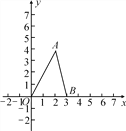
【题目】如图,在平面直角坐标系中,点A的坐标为(2,4),点B的坐标为(3,0).三角形AOB中任意一点P(x0,y0)经平移后的对应点为P1(x0+2,y0),并且点A,O,B的对应点分别为点D,E,F.
(1)指出平移的方向和距离;
(2)画出平移后的三角形DEF;
(3)求线段OA在平移过程中扫过的面积.
参考答案:
【答案】(1)把三角形AOB沿x轴正方向(即向右)平移2个单位长度;(2)图见解析; (3)所求面积为8.
【解析】试题分析:对于(1),根据点坐标向右平移时其纵坐标不变,横坐标加平移单位即可正确解答;
对于(2),由平移的规律找到点A,O,B的对应点D,E,F,顺序连接即可;
对于(3),由题意知,线段OA在平移过程中扫过的图形是平行四边形,由平行四边形的面积计算公式直接解答即可.
解:(1)把三角形AOB沿x轴正方向(即向右)平移2个单位长度.
(2)如图.
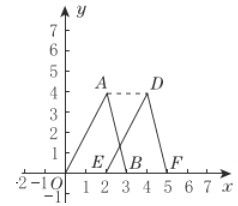
(3)连接AD,线段OA在平移过程中扫过的面积是平行四边形AOED的面积,∴所求面积为2×4=8.
-
科目: 来源: 题型:
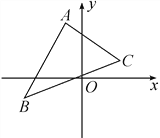
查看答案和解析>>【题目】如图,已知三角形ABC的三个顶点的坐标分别为A(-1,3),B(-3,-1),C(2,1),求三角形ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形网格中,每个小正方形的边长都为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移后得△DEF,使点A的对应点为点D,点B的对应点为点E.
(1)画出△DEF;
(2)连接AD、BE,则线段AD与BE的关系是 ;
(3)求△DEF的面积.

-
科目: 来源: 题型:
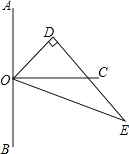
查看答案和解析>>【题目】如图,点O在直线AB上,OC⊥AB,△ODE中,∠ODE=90°,∠EOD=60°,先将△ODE一边OE与OC重合,然后绕点O顺时针方向旋转,当OE与OB重合时停止旋转.
(1)当OD在OA与OC之间,且∠COD=20°时,则∠AOE=______;
(2)试探索:在△ODE旋转过程中,∠AOD与∠COE大小的差是否发生变化?若不变,请求出这个差值;若变化,请说明理由;
(3)在△ODE的旋转过程中,若∠AOE=7∠COD,试求∠AOE的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在某市城区地图(比例尺1∶9000)上,新安大街的图上长度与光华大街的图上长度分别是16 cm,10 cm.
(1)新安大街与光华大街的实际长度各是多少米?
(2)新安大街与光华大街的图上长度之比是多少?它们的实际长度之比呢?你发现了什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:平面内的直线l1与l2相交于点O,对于该平面内任意一点M,点M到直线l1、l2的距离分别为a、b,则称有序非负实数对(a,b)是点M的“距离坐标”,根据上述定义,距离坐标为(2,1)的点的个数有( )
A. 2个B. 3个C. 4个D. 5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题:

⑴ 作出△
 绕点A逆时针旋转90°的△AB1C1,再作出△AB1C1关于原点O成中心对称的△A1B2C2.
绕点A逆时针旋转90°的△AB1C1,再作出△AB1C1关于原点O成中心对称的△A1B2C2.(2)请直接写出以A1、B2、C2为顶点的平行四边形的第四个顶点D的坐标 .(写出一个即可)
相关试题

