【题目】已知,如图四边形AOBC为正方形,点C的坐标为(4 ![]() ,0),动点P沿着折线OACB的方向以1个单位每秒的速度匀速运动,同时点Q沿着折线OBCA的方向匀速运动,速度是2个单位长度每秒,运动时间为t秒,当他们相遇时同时停止运动.
,0),动点P沿着折线OACB的方向以1个单位每秒的速度匀速运动,同时点Q沿着折线OBCA的方向匀速运动,速度是2个单位长度每秒,运动时间为t秒,当他们相遇时同时停止运动.
(1)点A的坐标是正方形AOBC的面积是 .
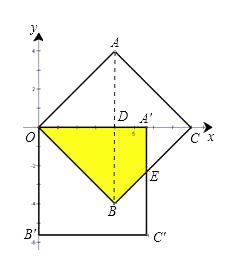
(2)将正方形绕点O顺时针旋转45°,求旋转后的正方形与原正方形的重叠部分的面积.
(3)运动时间t为多少秒时,以A、P、B、Q四点为顶点的四边形为平行四边形?
(4)是否存在这样的t值,使△OPQ成为等腰三角形?若存在,请求出t的值;若不存在,请说明理由.
参考答案:
【答案】
(1)(2![]() ,2
,2![]() );16
);16
(2)
由OC=4![]() 得,OA=OB=OC=AC=4,
得,OA=OB=OC=AC=4,
旋转后可得OA′=OA=4,
∴A′C=4![]() -4,而可知∠CA′E=90°,∠OCB=45°,
-4,而可知∠CA′E=90°,∠OCB=45°,
∴△A′EC是等腰直角三角形,
∴A′E=A′C=4![]() -4,
-4,
∴S四边形OA’EB=S△OBC-S△A’EC=16![]() -16.
-16.
(3)
解:当P在OA,Q在OB时,不存在;
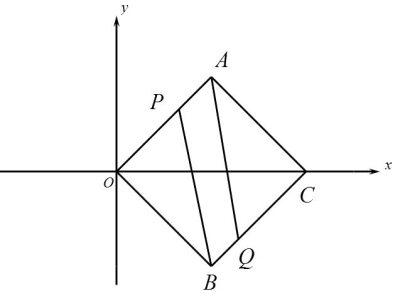
当P在OA,Q在BC时,当AP=BQ时,又因为AO//BC,则四边形APBQ为平行四边形,如图,
AP=4-t,BQ =2t-4,
则4-t=2t-4,
解得t=![]() .
.
即当t=![]() 时,四边形APBQ是平行四边形.
时,四边形APBQ是平行四边形.
(4)
存在,当Q点在BC上时,使OQ=QP,QM为OP的垂直平分线,
则有OP=2OM=2BQ,而OP=t,BQ=4-2t,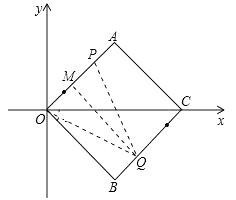
∴t=2(4-2t),
∴t=![]() .
.
【解析】(1)在正方形OACB中,连接AB,交OC于D点,则OD=AD=![]() OC=2
OC=2![]() ,即A(2
,即A(2![]() ,2
,2![]() ).
).
正方形的面积为:![]() =16.
=16.
所以答案是:(2![]() ,2
,2![]() );16.
);16.
【考点精析】通过灵活运用等腰三角形的判定和平行四边形的判定,掌握如果一个三角形有两个角相等,那么这两个角所对的边也相等(简称:等角对等边).这个判定定理常用于证明同一个三角形中的边相等;两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形即可以解答此题.
-
科目: 来源: 题型:
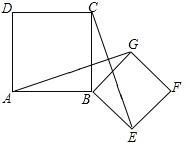
查看答案和解析>>【题目】如图,四边形ABCD、BEFG均为正方形,连接AG、CE.
(1)求证:AG=CE;
(2)求证:AG⊥CE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,AD⊥BC于点D,∠1=∠2,∠CDG=∠B,求证:EF⊥BC.
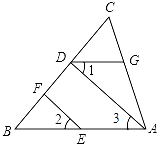
-
科目: 来源: 题型:
查看答案和解析>>【题目】预计下届世博会将吸引约69000000人次参观,将69000000用科学记数法表示正确的是( )
A.0.69×108
B.6.9×107
C.6.9×106
D.69×106 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,OA⊥OC,OB⊥OD,下面结论:①∠AOB=∠COD;②∠AOB+∠COD=90°;③∠BOC+∠AOD=180°;④∠AOC﹣∠COD=∠BOC中,正确的有(填序号).
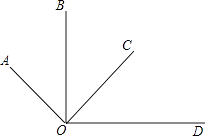
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种肥皂原零售价每块2元,凡购买2块以上(包括2块),商场推出两种优惠销售办法.第一种:一块肥皂按原价,其余按原价的七折销售;第二种:全部按原价的八折销售.你在购买相同数量肥皂的情况下,要使第一种方法比第二种方法得到的优惠多,最少需要买( )块肥皂.
A. 5 B. 4 C. 3 D. 2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AB∥CD,∠ABC=∠ADC,DE垂直于对角线AC,垂足是E,连接BE.
(1)求证:四边形ABCD是平行四边形;
(2)若点E是AC的中点,判断BE与AC的位置关系,并说明理由;
(3)若△ABE是等边三角形,AD=
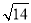 ,求对角线AC的长.
,求对角线AC的长.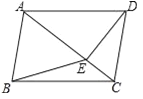
相关试题

