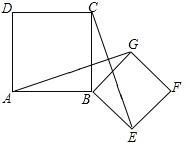
【题目】如图,四边形ABCD、BEFG均为正方形,连接AG、CE.
(1)求证:AG=CE;
(2)求证:AG⊥CE.
参考答案:
【答案】(1)证明见试题解析;(2)证明见试题解析.
【解析】
试题分析:(1)由ABCD、BEFG均为正方形,得出AB=CB,∠ABC=∠GBE=90°,BG=BE,得出∠ABG=∠CBE,从而得到△ABG≌△CBE,即可得到结论;
(2)由△ABG≌△CBE,得出∠BAG=∠BCE,由∠BAG+∠AMB=90°,对顶角∠AMB=∠CMN,得出∠BCE+∠CMN=90°,证出∠CNM=90°即可.
试题解析:(1)∵四边形ABCD、BEFG均为正方形,∴AB=CB,∠ABC=∠GBE=90°,BG=BE,∴∠ABG=∠CBE,在△ABG和△CBE中,∵AB=CB,∠ABG=∠CBE,BG=BE,∴△ABG≌△CBE(SAS),∴AG=CE;
(2)如图所示:∵△ABG≌△CBE,∴∠BAG=∠BCE,∵∠ABC=90°,∴∠BAG+∠AMB=90°,∵∠AMB=∠CMN,∴∠BCE+∠CMN=90°,∴∠CNM=90°,∴AG⊥CE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点(﹣4,4)在第象限.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F.
(1)PC=PE;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图.△ABC中,AB=AC,AB的垂直平分线交AC于P点,若AB=6cm,BC=4cm,△PBC的周长等于( )
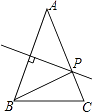
A.4cm
B.6cm
C.8cm
D.10cm -
科目: 来源: 题型:
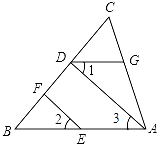
查看答案和解析>>【题目】已知:如图,AD⊥BC于点D,∠1=∠2,∠CDG=∠B,求证:EF⊥BC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】预计下届世博会将吸引约69000000人次参观,将69000000用科学记数法表示正确的是( )
A.0.69×108
B.6.9×107
C.6.9×106
D.69×106 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图四边形AOBC为正方形,点C的坐标为(4
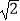 ,0),动点P沿着折线OACB的方向以1个单位每秒的速度匀速运动,同时点Q沿着折线OBCA的方向匀速运动,速度是2个单位长度每秒,运动时间为t秒,当他们相遇时同时停止运动.
,0),动点P沿着折线OACB的方向以1个单位每秒的速度匀速运动,同时点Q沿着折线OBCA的方向匀速运动,速度是2个单位长度每秒,运动时间为t秒,当他们相遇时同时停止运动.
(1)点A的坐标是正方形AOBC的面积是 .
(2)将正方形绕点O顺时针旋转45°,求旋转后的正方形与原正方形的重叠部分的面积.
(3)运动时间t为多少秒时,以A、P、B、Q四点为顶点的四边形为平行四边形?
(4)是否存在这样的t值,使△OPQ成为等腰三角形?若存在,请求出t的值;若不存在,请说明理由.
相关试题

