【题目】如图,OA⊥OC,OB⊥OD,下面结论:①∠AOB=∠COD;②∠AOB+∠COD=90°;③∠BOC+∠AOD=180°;④∠AOC﹣∠COD=∠BOC中,正确的有(填序号).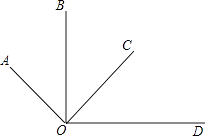
参考答案:
【答案】①③④
【解析】解:∵OA⊥OC,OB⊥OD,
∴∠AOC=∠BOD=90°,
∴∠AOB+∠BOC=∠COD+∠BOC=90°,
∴∠AOB=∠COD,故①正确;
∠AOB+∠COD不一定等于90°,故②错误;
∠BOC+∠AOD=90°﹣∠AOB+90°+∠AOB=180°,故③正确;
∠AOC﹣∠COD=∠AOC﹣∠AOB=∠BOC,故④正确;
综上所述,说法正确的是①③④.
所以答案是:①③④.
【考点精析】认真审题,首先需要了解余角和补角的特征(互余、互补是指两个角的数量关系,与两个角的位置无关).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,AD⊥BC于点D,∠1=∠2,∠CDG=∠B,求证:EF⊥BC.
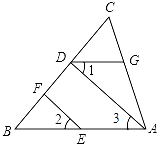
-
科目: 来源: 题型:
查看答案和解析>>【题目】预计下届世博会将吸引约69000000人次参观,将69000000用科学记数法表示正确的是( )
A.0.69×108
B.6.9×107
C.6.9×106
D.69×106 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图四边形AOBC为正方形,点C的坐标为(4
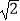 ,0),动点P沿着折线OACB的方向以1个单位每秒的速度匀速运动,同时点Q沿着折线OBCA的方向匀速运动,速度是2个单位长度每秒,运动时间为t秒,当他们相遇时同时停止运动.
,0),动点P沿着折线OACB的方向以1个单位每秒的速度匀速运动,同时点Q沿着折线OBCA的方向匀速运动,速度是2个单位长度每秒,运动时间为t秒,当他们相遇时同时停止运动.
(1)点A的坐标是正方形AOBC的面积是 .
(2)将正方形绕点O顺时针旋转45°,求旋转后的正方形与原正方形的重叠部分的面积.
(3)运动时间t为多少秒时,以A、P、B、Q四点为顶点的四边形为平行四边形?
(4)是否存在这样的t值,使△OPQ成为等腰三角形?若存在,请求出t的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某种肥皂原零售价每块2元,凡购买2块以上(包括2块),商场推出两种优惠销售办法.第一种:一块肥皂按原价,其余按原价的七折销售;第二种:全部按原价的八折销售.你在购买相同数量肥皂的情况下,要使第一种方法比第二种方法得到的优惠多,最少需要买( )块肥皂.
A. 5 B. 4 C. 3 D. 2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AB∥CD,∠ABC=∠ADC,DE垂直于对角线AC,垂足是E,连接BE.
(1)求证:四边形ABCD是平行四边形;
(2)若点E是AC的中点,判断BE与AC的位置关系,并说明理由;
(3)若△ABE是等边三角形,AD=
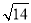 ,求对角线AC的长.
,求对角线AC的长.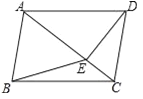
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB与CD相交于点O,∠A=∠AOC,∠B=∠BOD.
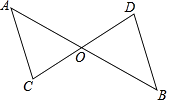
求证:∠C=∠D.
证明:∵∠A=∠AOC,∠B=∠BOD(已知)
又∠AOC=∠BOD()
∴∠A=∠B()
∴AC∥BD()
∴∠C=∠D()
相关试题

