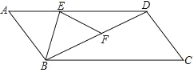
【题目】.E为□ABCD边AD上一点,将ABE沿BE翻折得到FBE,点F在BD上,且EF=DF.若∠C=52°,则∠ABE=____.
参考答案:
【答案】51°
【解析】
由平行四边形的性质和折叠的性质得出∠BFE=∠A=52°,∠FBE=∠ABE,由等腰三角形的性质和三角形的外角性质得出∠EDF=∠DEF=![]() ∠BFE=26°,由三角形内角和定理求出∠ABD=102°,即可得出∠ABE的度数.
∠BFE=26°,由三角形内角和定理求出∠ABD=102°,即可得出∠ABE的度数.
∵四边形ABCD为平行四边形,
∴∠A=∠C=52°,AD∥BC.
由折叠的性质可得∠ABE=∠FBE,∠A=∠BFE=52°,
∵EF=DF,
∴∠FED=∠EDF,
∴∠EFB=∠FED+∠EDF=2∠EDF=52°,即∠EDF=26°.
∵AD∥BC,
∴∠CBD=∠EDF=26°,∠ABC=180°-∠A=128°,
∴∠ABF=∠ABC-∠CBD=128°-26°=102°.
又∵∠ABE=∠FBE,
∴∠ABE=![]() ∠ABF=
∠ABF= ![]() ×102°=51°.
×102°=51°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将ABCD沿CE折叠,使点D落在BC边上的F处,点E在AD上.
(1)求证:四边形ABFE为平行四边形;
(2)若AB=4,BC=6,求四边形ABFE的周长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:sin245°﹣2tan30°tan60°+cos245°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组:
 请结合题意填空,完成本题的解答:
请结合题意填空,完成本题的解答:
(i)解不等式(1),得;
(ii)解不等式(2),得;
(iii)把不等式(1)和(2)的解集在数轴上表示出来:
(iv)原不等式的解集为: . -
科目: 来源: 题型:
查看答案和解析>>【题目】某校申报“跳绳特色运动”学校一年后,抽样调查了部分学生的“1分钟跳绳”成绩,并制成了下面的频数分布直方图(每小组含最小值,不含最大值)和扇形图.
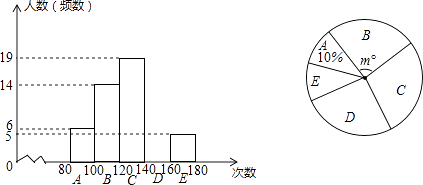
(1)补全频数分布直方图,扇形图中m=;
(2)若把每组中各个数据用这组数据的中间值代替(如A组80≤x<100的中间值是 =90次),则这次调查的样本平均数是多少?
=90次),则这次调查的样本平均数是多少?
(3)如果“1分钟跳绳”成绩大于或等于120次为优秀,那么该校2100名学生中“1分钟跳绳”成绩为优秀的大约有多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列式子:
0×2+1=12……①
1×3+1=22……②
2×4+1=32……③
3×5+1=42……④
……
(1)第⑤个式子 ,第⑩个式子 ;
(2)请用含n(n为正整数)的式子表示上述的规律,并证明:
(3)求值:(1+
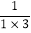 )(1+
)(1+ )(1+
)(1+ )(1+
)(1+ )…(1+
)…(1+ ).
). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,∠ADC=900,∠BAD=600,对角线AC平分∠BAD,且AB=AC=4,点E、F分别是AC、BC的中点,连接DE,EF,DF,则DF的长为_______.

相关试题

