Question

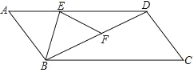
【题目】如图，将ABCD沿CE折叠，使点D落在BC边上的F处，点E在AD上．

（1）求证：四边形ABFE为平行四边形；

（2）若AB=4，BC=6，求四边形ABFE的周长．

Answer 1

【答案】（1）证明见解析；（2）12.

【解析】

（1）根据折叠的性质得到EF=ED，∠CFE=∠CDE，根据平行四边形的性质得到AD∥BC，∠B=∠D，由平行线的判定得到AE∥BF，即可得到结论；
（2）根据平行四边形的性质得到EF=AB=4．求得ED=4，得到AE=BF=6-4=2，于是得到结论．

（1）证明：∵将ABCD沿CE折叠，使点D落在BC边上的F处，∴EF=ED，∠CFE=∠CDE，

∵四边形ABCD是平行四边形，∴AD∥BC，∠B=∠D，∴AE∥BF，∠B=∠CFE，

∴AB∥EF，∴四边形ABFE为平行四边形；

（2）解：∵四边形ABFE为平行四边形，∴EF=AB=4，

∵EF=ED，∴ED=4，∴AE=BF=6﹣4=2，∴四边形ABFE的周长=AB+BF+EF+EA=12．