【题目】观察下列式子:
0×2+1=12……①
1×3+1=22……②
2×4+1=32……③
3×5+1=42……④
……
(1)第⑤个式子 ,第⑩个式子 ;
(2)请用含n(n为正整数)的式子表示上述的规律,并证明:
(3)求值:(1+![]() )(1+
)(1+![]() )(1+
)(1+![]() )(1+
)(1+![]() )…(1+
)…(1+![]() ).
).
参考答案:
【答案】(1)4×6+1=52,9×11+1=102;(2)(n﹣1)(n+1)+1=n2;(3)![]() .
.
【解析】
(1)观察发现一个正整数乘以比这个正整数大2的数再加1就等于这个正整数加1的平方;
(2)根据(1)中发现的规律解答即可;
(3)先通分,然后根据(2)中结论解答即可.
解:(1)第⑤个式子为4×6+1=52,第⑩个式子9×11+1=102,
故答案为:4×6+1=52,9×11+1=102;
(2)第n个式子为(n﹣1)(n+1)+1=n2,
证明:左边=n2﹣1+1=n2,
右边=n2,
∴左边=右边,
即(n﹣1)(n+1)+1=n2.
(3)原式=![]() ×
×![]() ×
×![]() ×…×
×…×![]()
=![]()
=![]()
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组:
 请结合题意填空,完成本题的解答:
请结合题意填空,完成本题的解答:
(i)解不等式(1),得;
(ii)解不等式(2),得;
(iii)把不等式(1)和(2)的解集在数轴上表示出来:
(iv)原不等式的解集为: . -
科目: 来源: 题型:
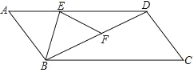
查看答案和解析>>【题目】.E为□ABCD边AD上一点,将ABE沿BE翻折得到FBE,点F在BD上,且EF=DF.若∠C=52°,则∠ABE=____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校申报“跳绳特色运动”学校一年后,抽样调查了部分学生的“1分钟跳绳”成绩,并制成了下面的频数分布直方图(每小组含最小值,不含最大值)和扇形图.
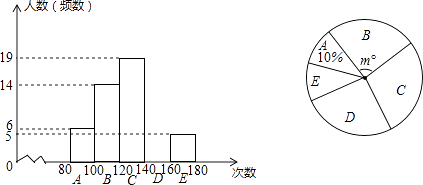
(1)补全频数分布直方图,扇形图中m=;
(2)若把每组中各个数据用这组数据的中间值代替(如A组80≤x<100的中间值是 =90次),则这次调查的样本平均数是多少?
=90次),则这次调查的样本平均数是多少?
(3)如果“1分钟跳绳”成绩大于或等于120次为优秀,那么该校2100名学生中“1分钟跳绳”成绩为优秀的大约有多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,∠ADC=900,∠BAD=600,对角线AC平分∠BAD,且AB=AC=4,点E、F分别是AC、BC的中点,连接DE,EF,DF,则DF的长为_______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC在平面直角坐标系中的位置如图所示,先将△ABC向右平移3个单位,再向下平移1个单位到△A1B1C1,△A1B1C1和△A2B2C2关于x轴对称

(1)画出△A1B1C1和△A2B2C2
(2)在x轴上确定一点P,使BP+A1P的值最小,直接写出P的坐标为________
(3)点Q在坐标轴上且满足△ACQ为等腰三角形,则这样的Q点有 个
-
科目: 来源: 题型:
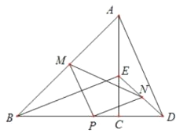
查看答案和解析>>【题目】如图,已知等腰Rt△ABC和△CDE,AC=BC,CD=CE,连接BE、AD,P为BD中点,M为AB中点、N为DE中点,连接PM、PN、MN.
(1)试判断△PMN的形状,并证明你的结论;
(2)若CD=5,AC=12,求△PMN的周长.
相关试题

