【题目】抛物线y=ax2+bx+c上,部分点的横、纵坐标x、y的对应值如下表:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | ﹣4 | ﹣4 | 0 | 8 |
(1)根据上表填空; ①方程ax2+bx+c=0的两个根分别是和 .
②抛物线经过点(﹣3,);
③在对称轴左侧,y随x增大而;
(2)求抛物线y=ax2+bx+c的解析式.
参考答案:
【答案】
(1)x1=﹣2;x2=1;8;减小
(2)解:设抛物线解析式为y=ax2+bx+c,
把(﹣2,0),(1,0)、(0,﹣4)代入得: 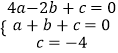 ,
,
解得: 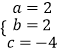 ,
,
则抛物线解析式为y=2x2+2x﹣4
【解析】解:(1)①观察表格得:方程ax2+bx+c=0的两个根分别是x1=﹣2和x2=1;②抛物线经过点(﹣3,8);③在对称轴左侧,y随x的增大而减小; 所以答案是:①x1=﹣2,x2=1;②8;③减小;
【考点精析】认真审题,首先需要了解抛物线与坐标轴的交点(一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.).
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程:
(1)x2+x=0;
(2)x2﹣4x﹣1=0. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图为一段圆弧形弯道,弯道长12π米,圆弧所对的圆心角是81°.

(1)用直尺和圆规作出圆弧所在的圆心O;(不写作法,保留作图痕迹)
(2)求这段圆弧的半径R. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,点O是边长为2的正方形ABCD的中心.

(1)若函数y=x2+m的图象过点C,求这个函数的解析式;并判断其函数图象是否过A点.
(2)若将(1)中的函数图象先向右平移1个单位,再向上平移2个单位,直接写出平移后函数的解析式和顶点坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△OAB中,OA=OB=10,∠AOB=70°,以点O为圆心,6为半径的优弧
 分别交OA、OB于点M,N.
分别交OA、OB于点M,N. 
(1)点P在右半弧上(∠BOP是锐角),将OP绕点O逆时针旋转70°得OP′.求证:AP=BP′;
(2)点T在左半弧上,若AT与弧相切,求点T到OA的距离;
(3)设点Q在优弧 上,当△AOQ的面积最大时,直接写出∠BOQ的度数.
上,当△AOQ的面积最大时,直接写出∠BOQ的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】在同一平面直角坐标系中,函数y=ax+b与y=ax2﹣bx的图象可能是( )
A.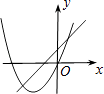
B.
C.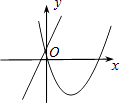
D.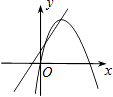
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函y=ax2+bx+c(a≠0)图象的一部分,对称轴为直线x=
 ,且经过点(2,0),下列说法: ①abc<0;
,且经过点(2,0),下列说法: ①abc<0;
②a+b=0;
③4a+2b+c<0;
④若(﹣2,y1),(﹣3,y2)是抛物线上的两点,则y1<y2 ,
其中说法正确的是( )
A.①②④
B.③④
C.①③④
D.①②
相关试题

