【题目】如图,折叠边长为a的正方形ABCD,使点C落在边AB上的点M处(不与点A,B重合),点D落在点N处,折痕EF分别与边BC、AD交于点E、F,MN与边AD交于点G.证明:
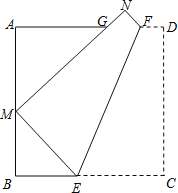
(1)△AGM∽△BME;
(2)若M为AB中点,则![]() =
=![]() =
=![]() ;
;
(3)△AGM的周长为2a.
参考答案:
【答案】见解析
【解析】
试题分析:(1)根据正方形的性质和折叠的性质得出∠A=∠B,∠AGM=∠BME,再利用相似三角形的判定证明即可;
(2)设BE=x,利用勾股定理得出x的值,再利用相似三角形的性质证明即可;
(3)设BM=x,AM=a﹣x,利用勾股定理和相似三角形的性质证明即可.
证明:(1)∵四边形ABCD是正方形,
∴∠A=∠B=∠C=90°,
∴∠AMG+∠AGM=90°,
∵EF为折痕,
∴∠GME=∠C=90°,
∴∠AMG+∠BME=90°,
∴∠AGM=∠BME,
在△AGM与△BME中,
∵∠A=∠B,∠AGM=∠BME,
∴△AGM∽△BME;
(2)∵M为AB中点,
∴BM=AM=![]() ,
,
设BE=x,则ME=CE=a﹣x,
在Rt△BME中,∠B=90°,
∴BM2+BE2=ME2,即(![]() )2+x2=(a﹣x)2,
)2+x2=(a﹣x)2,
∴x=![]() a,
a,
∴BE=![]() a,ME=
a,ME=![]() a,
a,
由(1)知,△AGM∽△BME,
∴![]() =
=![]() =
=![]() =
=![]() ,
,
∴AG=![]() BM=
BM=![]() a,GM=
a,GM=![]() ME=
ME=![]() a,
a,
∴![]() =
=![]() =
=![]() ;
;
(3)设BM=x,则AM=a﹣x,ME=CE=a﹣BE,
在Rt△BME中,∠B=90°,
∴BM2+BE2=ME2,即x2+BE2=(a﹣BE)2,
解得:BE=![]() ﹣
﹣![]() ,
,
由(1)知,△AGM∽△BME,
∴![]() =
=![]() =
=![]() ,
,
∵C△BME=BM+BE+ME=BM+BE+CE=BM+BC=a+x,
∴C△AGM=C△BME![]() =(a+x)
=(a+x)![]() =2a.
=2a.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,M、N分别是边AD、BC的中点,点P、Q在DC边上,且PQ=
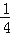 DC.若AB=16,BC=20,则图中阴影部分的面积是 .
DC.若AB=16,BC=20,则图中阴影部分的面积是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】分析探索题:细心观察如图,认真分析各式,然后解答问题.
OA22=(
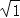 )2+1=2 S1=
)2+1=2 S1=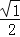 ;
;OA32=(
 )2+1=3 S2=
)2+1=3 S2=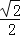 ;
;OA42=(
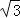 )2+1=4 S3=
)2+1=4 S3=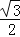 …
…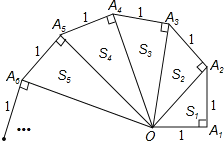
(1)请用含有n(n为正整数)的等式Sn= ;
(2)推算出OA10= .
(3)求出 S12+S22+S32+…+S102的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题背景:在△ABC中,AB、BC、AC三边的长分别为
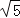 、
、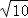 、
、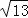 ,求这个三角形的面积小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.
,求这个三角形的面积小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.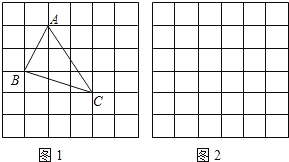
(1)请你将△ABC的面积直接填写在横线上.
(2)画△DEF,DE、EF、DF三边的长分别为
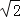 、
、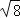 、
、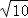
①判断三角形的形状,说明理由.
②求这个三角形的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】803﹣80能被( )整除.
A. 76 B. 78 C. 79 D. 82
-
科目: 来源: 题型:
查看答案和解析>>【题目】课本1.4有这样一道例题:
问题4:用一根长22cm的铁丝:
(1)能否围成面积是30cm2的矩形?
(2)能否围成面积是32cm2的矩形?
据此,一位同学提出问题:“用这根长22cm的铁丝能否围成面积最大的矩形?若能围成,求出面积最大值;若不能围成,请说明理由.”请你完成该同学提出的问题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在半径为2的⊙O中,弦AB长为2.

(1)求点O到AB的距离.
(2)若点C为⊙O上一点(不与点A,B重合),求∠BCA的度数.
相关试题

