【题目】分析探索题:细心观察如图,认真分析各式,然后解答问题.
OA22=(![]() )2+1=2 S1=
)2+1=2 S1=![]() ;
;
OA32=(![]() )2+1=3 S2=
)2+1=3 S2=![]() ;
;
OA42=(![]() )2+1=4 S3=
)2+1=4 S3=![]() …
…
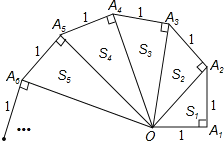
(1)请用含有n(n为正整数)的等式Sn= ;
(2)推算出OA10= .
(3)求出 S12+S22+S32+…+S102的值.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)S12+S22+S32+…+S102=
;(3)S12+S22+S32+…+S102=![]() .
.
【解析】
试题分析:(1)此题要利用直角三角形的面积公式,观察上述结论,会发现,第n个图形的一直角边就是![]() ,然后利用面积公式可得.
,然后利用面积公式可得.
(2)由同述OA2=![]() ,0A3=
,0A3=![]() …可知OA10=
…可知OA10=![]() .
.
(3)S12+S22+S32+…+S102的值就是把面积的平方相加就可.
解:(1)![]() +1=n+1
+1=n+1
Sn=![]() (n是正整数);
(n是正整数);
故答案是:![]() ;
;
(2)∵OA12=1,
OA22=(![]() )2+1=2,
)2+1=2,
OA32=(![]() )2+1=3,
)2+1=3,
OA42=(![]() )2+1=4,
)2+1=4,
∴OA12=![]() ,
,
OA2=![]() ,
,
OA3=![]() ,…
,…
∴OA10=![]() ;
;
故答案是:![]() ;
;
(3)S12+S22+S32+…+S102
=(![]() )2+(
)2+(![]() )2+(
)2+(![]() )2+…+(
)2+…+(![]() )2
)2
=![]() (1+2+3+…+10)
(1+2+3+…+10)
=![]() .
.
即:S12+S22+S32+…+S102=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形的两边长分别为3cm和7cm,则周长为( )
A.13 cm B.17 cm C.13 cm或17 cm D.11 cm或17 cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】射击队为从甲、乙两名运动员中选拔一人参加比赛,对他们进行了六次测试,测试成绩如下表(单位:环):
第一次
第二次
第三次
第四次
第五次
第六次
平均成绩
中位数
甲
10
8
9
8
10
9
9
①
乙
10
7
10
10
9
8
②
9.5
(1)完成表中填空① ;② ;
(2)请计算甲六次测试成绩的方差;
(3)若乙六次测试成绩方差为
 ,你认为推荐谁参加比赛更合适,请说明理由.
,你认为推荐谁参加比赛更合适,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,M、N分别是边AD、BC的中点,点P、Q在DC边上,且PQ=
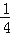 DC.若AB=16,BC=20,则图中阴影部分的面积是 .
DC.若AB=16,BC=20,则图中阴影部分的面积是 .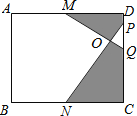
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题背景:在△ABC中,AB、BC、AC三边的长分别为
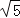 、
、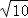 、
、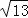 ,求这个三角形的面积小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.
,求这个三角形的面积小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.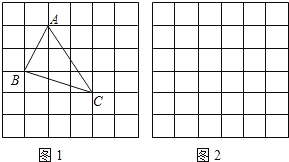
(1)请你将△ABC的面积直接填写在横线上.
(2)画△DEF,DE、EF、DF三边的长分别为
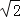 、
、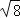 、
、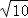
①判断三角形的形状,说明理由.
②求这个三角形的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,折叠边长为a的正方形ABCD,使点C落在边AB上的点M处(不与点A,B重合),点D落在点N处,折痕EF分别与边BC、AD交于点E、F,MN与边AD交于点G.证明:
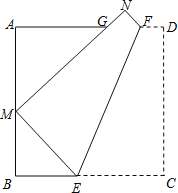
(1)△AGM∽△BME;
(2)若M为AB中点,则
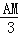 =
=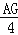 =
=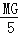 ;
;(3)△AGM的周长为2a.
-
科目: 来源: 题型:
查看答案和解析>>【题目】803﹣80能被( )整除.
A. 76 B. 78 C. 79 D. 82
相关试题

