【题目】如图,在半径为2的⊙O中,弦AB长为2.

(1)求点O到AB的距离.
(2)若点C为⊙O上一点(不与点A,B重合),求∠BCA的度数.
参考答案:
【答案】(1)点O到AB的距离为![]() ;(2)∠BCA的度数为30°或150°.
;(2)∠BCA的度数为30°或150°.
【解析】
试题分析:(1)过点O作OC⊥AB于点C,证出△OAB是等边三角形,继而求得∠AOB的度数,然后由三角函数的性质,求得点O到AB的距离;
(2)证出△ABO是等边三角形得出∠AOB=60°. 再分两种情况:点C在优弧![]() 上,则∠BCA=30°;点C在劣弧
上,则∠BCA=30°;点C在劣弧![]() 上,则∠BCA=
上,则∠BCA=![]() (360°﹣∠AOB)=150°;即可得出结果.
(360°﹣∠AOB)=150°;即可得出结果.
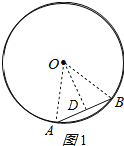
解:(1)过点O作OD⊥AB于点D,连接AO,BO.如图1所示:
∵OD⊥AB且过圆心,AB=2,
∴AD=![]() AB=1,∠ADO=90°,
AB=1,∠ADO=90°,
在Rt△ADO中,∠ADO=90°,AO=2,AD=1,
∴OD=![]() =
=![]() .
.
即点O到AB的距离为![]() .
.
(2)如图2所示:
∵AO=BO=2,AB=2,
∴△ABO是等边三角形,
∴∠AOB=60°.
若点C在优弧![]() 上,则∠BCA=30°;
上,则∠BCA=30°;
若点C在劣弧![]() 上,则∠BCA=
上,则∠BCA=![]() (360°﹣∠AOB)=150°;
(360°﹣∠AOB)=150°;
综上所述:∠BCA的度数为30°或150°.
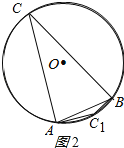
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,折叠边长为a的正方形ABCD,使点C落在边AB上的点M处(不与点A,B重合),点D落在点N处,折痕EF分别与边BC、AD交于点E、F,MN与边AD交于点G.证明:
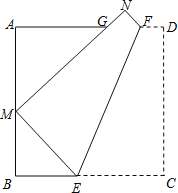
(1)△AGM∽△BME;
(2)若M为AB中点,则
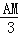 =
=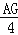 =
=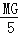 ;
;(3)△AGM的周长为2a.
-
科目: 来源: 题型:
查看答案和解析>>【题目】803﹣80能被( )整除.
A. 76 B. 78 C. 79 D. 82
-
科目: 来源: 题型:
查看答案和解析>>【题目】课本1.4有这样一道例题:
问题4:用一根长22cm的铁丝:
(1)能否围成面积是30cm2的矩形?
(2)能否围成面积是32cm2的矩形?
据此,一位同学提出问题:“用这根长22cm的铁丝能否围成面积最大的矩形?若能围成,求出面积最大值;若不能围成,请说明理由.”请你完成该同学提出的问题.
-
科目: 来源: 题型:
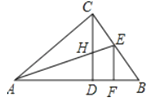
查看答案和解析>>【题目】如图,Rt△ABC中,∠ACB=90°,CD是斜边AB上的高,角平分线AE交CD于H,EF⊥AB于F,下列结论:①∠ACD=∠B;②CH=CE=EF;③AC=AF;④CH=HD.其中正确的结论为( )
A.①②④ B.①②③ C.②③ D.①③
-
科目: 来源: 题型:
查看答案和解析>>【题目】一只不透明的袋子中,装有三个分别标记为“1”、“2”、“3”的球,这三个球除了标记不同外,其余均相同.搅匀后,从中摸出一个球,记录球上的标记后放回袋中并搅匀,再从中摸出一个球,再次记录球上的标记.
(1)请列出上述实验中所记录球上标记的所有可能的结果;
(2)求两次记录球上标记均为“1”的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
若直角三角形的两直角边之和为7,面积为6,则斜边长为_________.
相关试题

