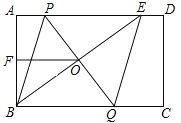
【题目】如图,在矩形ABCD中,E是AD上一点,PQ垂直平分BE,分别交AD、BE、BC于点P、O、Q,连接BP、EQ.
(1)求证:四边形BPEQ是菱形;
(2)若AB=6,F为AB的中点,OF+OB=9,求PQ的长.
参考答案:
【答案】(1)证明见解析;(2)PQ的长是![]() .
.
【解析】试题分析:⑴先根据线段垂直平分线的性质证明QB=QE,由ASA证明△BOQ≌△EOP,得出PE=QB,证出四边形ABGE是平行四边形,再根据菱形的判定即可得出结论.
⑵根据三角形中位线的性质可得![]() ,设
,设![]() ,则
,则
![]() ,在Rt△ABE中,根据勾股定理可得
,在Rt△ABE中,根据勾股定理可得![]() ,解得BE=10,
,解得BE=10,
得到![]() ,设
,设![]() ,则
,则![]() ,
, ![]() ,计算得出
,计算得出![]() ,在Rt△BOP中,根据勾股定理可得
,在Rt△BOP中,根据勾股定理可得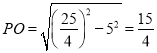 ,由
,由![]() 即可求解.
即可求解.
试题解析:
(1)证明:∵ PQ垂直平分BE,
∴ QB=QE,OB=OE,
∵ 四边形ABCD是矩形,
∴ AD∥BC,
∴ ∠ PEO=∠ QBO,
在△ BOQ与△ EOP中,
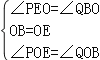 ,
,
∴ △ BOQ≌ △ EOP(ASA),
∴ PE=QB,
又∵ AD∥BC,
∴ 四边形BPEQ是平行四边形,
又∵ QB=QE,
∴ 四边形BPEQ是菱形;
(2)解:∵ O,F分别为PQ,AB的中点,
∴ AE+BE=2OF+2OB=18,
设AE=x,则BE=18﹣x,
在Rt△ ABE中,62+x2=(18﹣x)2,
解得x=8,
BE=18﹣x=10,
∴ OB=![]() BE=5,
BE=5,
设PE=y,则AP=8﹣y,BP=PE=y,
在Rt△ ABP中,62+(8﹣y)2=y2,解得y=![]() ,
,
在Rt△ BOP中,PO=![]() =
=![]() ,
,
∴ PQ=2PO=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市准备购进A、B两种品牌台灯,其中A每盏进价比B进价贵30元,A售价120元,B售价80元.已知用1040元购进的A数量与用650元购进B的数量相同.
(1)求A、B的进价;
(2)超市打算购进A、B台灯共100盏,要求A、B的总利润不得少于3400元,不得多于3550元,问有多少种进货方案?
(3)在(2)的条件下,该超市决定对A进行降价促销,A台灯每盏降价m(8<m<15)元,B不变,超市如何进货获利最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(1)(﹣2)2﹣(3﹣5)﹣
 +2×(﹣3);
+2×(﹣3);(2)|1﹣
 |+|
|+| ﹣
﹣ |+|
|+| ﹣2|;
﹣2|;(3)4(x+3)2﹣16=0;
(4)27(x﹣3)3=﹣8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知直线y=2x+2与y轴、x轴分别交于A、B两点,以B为直角顶点在第二象限作等腰Rt△ABC .
(1)求点C的坐标,并求出直线AC的关系式.
(2)如图2,直线CB交y轴于E,在直线CB上取一点D,连接AD,若AD=AC,求证:BE=DE.
(3)如图3,在(1)的条件下,直线AC交x轴于M,P(
 ,k)是线段BC上一点,在线段BM上是否存在一点N,使△BPN的面积等于△BCM面积的
,k)是线段BC上一点,在线段BM上是否存在一点N,使△BPN的面积等于△BCM面积的 ?若存在,请求出点N的坐标;若不存在,请说明理由.
?若存在,请求出点N的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 平分
平分 .
. 与FC会平行吗?说明理由.
与FC会平行吗?说明理由. 与BC的位置关系如何?为什么?
与BC的位置关系如何?为什么? 平分
平分 吗?为什么?
吗?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠AOB,作图.
步骤1:在OB上任取一点M,以点M为圆心,MO长为半径画半圆,分别交OA、OB于点P、Q;
步骤2:过点M作PQ的垂线交
 于点C;
于点C;步骤3:画射线OC.
则下列判断:①
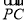 =
=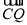 ;②MC∥OA;③OP=PQ;④OC平分∠AOB,其中正确的个数为( )
;②MC∥OA;③OP=PQ;④OC平分∠AOB,其中正确的个数为( )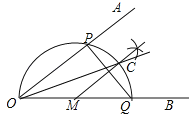
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形OABC是平行四边形,点C在x轴上,反比例函数y=
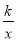 (x>0)的图象经过点A(5,12),且与边BC交于点D.若AB=BD,则点D的坐标为_____.
(x>0)的图象经过点A(5,12),且与边BC交于点D.若AB=BD,则点D的坐标为_____.
相关试题

