Question

【题目】矩形ABCD中，AB=3，AD=6，点E是边AD上的一个动点，把△BAE沿BE折叠，若点A的对应点A′恰落在矩形ABCD的对称轴上，则AE=_____．

Answer 1

【答案】3或．

【解析】

分两种情况：

①如图1，过A′作MN∥CD交AD于M，交BC于N，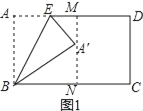

则直线MN是矩形ABCD 的对称轴，

∴AM=BN=AD=3，

∵△ABE沿BE折叠得到△A′BE，

∴A′E=AE，A′B=AB=3，

∴A′N==0，即A′与N重合，

∴A′M=3，

∴A′E2=EM2+A′M2，

∴A′E2=（3﹣A′E）2+32，

解得：A′E=3，

∴AE=3；

②如图2，过A′作PQ∥AD交AB于P，交CD于Q，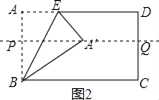

则直线PQ是矩形ABCD 的对称轴，

∴PQ⊥AB，AP=PB，AD∥PQ∥BC，

∴A′B=2PB，

∴∠PA′B=30°，

∴∠A′BC=30°，

∴∠EBA′=30°，

∴AE=A′E=A′B×tan30°=3×=；

综上所述：AE的长为3或；

故答案为：3或．