Question

【题目】如图，抛物线y=﹣x2+bx+c与x轴交于A、B两点，与y轴交于点C，已知点A（﹣1，0），点C（0，2）

（1）求抛物线的函数解析式；

（2）若D是抛物线位于第一象限上的动点，求△BCD面积的最大值及此时点D的坐标．

Answer 1

【答案】(1) 抛物线的函数解析式为y=﹣x2+x+2；(2)4；D（2，3）．

【解析】

（1）把A与C坐标代入抛物线解析式求出b与c的值，确定出解析式即可；

（2）连接OD，设出D坐标，四边形OCDB的面积等于三角形OCD面积+三角形OBD面积，表示出三角形BCD面积S与m的二次函数解析式，求出最大面积及D坐标即可．

（1）将点A（﹣1，0），点C（0，2）纵、横坐标分别代入y=﹣x2+bx+c得：

，

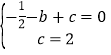解得：，

则抛物线的函数解析式为y=﹣x2+x+2；

（2）连接OD，则有B（4，0），设D（m，﹣m2+m+2），

∵S四边形OCDB﹣S△OCD﹣S△OBD=×2m+×4（﹣m2+m+2）=﹣m2+4m+4，

∴S△BCD=S四边形OCDB﹣S△OBC=﹣m2+4m+4﹣×4×2=﹣m2+4m=﹣（m﹣2）2+4，

当m=2时，S△BCD取得最大值4，

此时yD=﹣×4+×2+2=3，即D（2，3）．