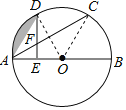
【题目】如图,C、D是半圆O上的三等分点,直径AB=4,连接AD、AC,DE⊥AB,垂足为E,DE交AC于点F.
(1)求∠AFE的度数;
(3)求阴影部分的面积(结果保留π和根号).

参考答案:
【答案】(1)∠AFE=60°;(2)S阴影=![]() π﹣
π﹣![]() .
.
【解析】试题分析:(1)连接OD,OC,根据已知条件得到∠AOD=∠DOC=∠COB=60°,根据圆周角定理得到∠CAB=30°,于是得到结论;
(2)由(1)知,∠AOD=60°,推出△AOD是等边三角形,OA=2,得到DE=![]() ,根据扇形和三角形的面积公式即可得到结论.
,根据扇形和三角形的面积公式即可得到结论.
试题解析:(1)连接OD,OC,
∵C、D是半圆O上的三等分点,∴![]() ,
,
∴∠AOD=∠DOC=∠COB=60°,∴∠CAB=30°,
∵DE⊥AB,∴∠AEF=90°,∴∠AFE=90°﹣30°=60°;
(2)由(1)知,∠AOD=60°,
∵OA=OD,AB=4,∴△AOD是等边三角形,OA=2,∵DE⊥AO,∴DE=![]() ,
,
∴S阴影=S扇形AOD﹣S△AOD=![]() ×2
×2![]() =
=![]() π﹣
π﹣![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】当x=1时,ax+b+1的值为3,则(a+b﹣1)(1﹣a﹣b)的值为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.a2a3=a6B.(ab3)2=a2b6
C.(a+2b)(a﹣2b)=a2﹣2b2D.a(ab﹣1)=a2b﹣1
-
科目: 来源: 题型:
查看答案和解析>>【题目】一艘货轮往返于上下游两个码头之间,逆流而上需要6小时,顺流而下需要4小时,若船在静水中的速度为20千米/时,则水流的速度是_____千米/时.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题是真命题的有( )
①过直线外一点,有且只有一条直线平行于已知直线;②同位角相等,两直线平 行;③内错角相等;④平面内垂直于同一直线的两直线平行.
A.1 个B.2 个C.3 个D.4 个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,∠B=30°,CD为AB边上的高,E是AB上一点,且CE=BE.
(1)写出图中所有的等腰三角形:______________________________
(2)写出图中所有的等边三角形:______________________________
(3)若DE=2cm,则AB=______cm,AC=______cm.

-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道,经过原点的抛物线可以用y=ax2+bx(a≠0)表示,对于这样的抛物线:
(1)当抛物线经过点(﹣2,0)和(﹣1,3)时,求抛物线的表达式;
(2)当抛物线的顶点在直线y=﹣2x上时,求b的值;
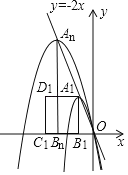
(3)如图,现有一组这样的抛物线,它们的顶点A1、A2、…,An在直线y=﹣2x上,横坐标依次为﹣1,﹣2,﹣3,…,﹣n(n为正整数,且n≤12),分别过每个顶点作x轴的垂线,垂足记为B1、B2,…,Bn,以线段AnBn为边向左作正方形AnBnCnDn,如果这组抛物线中的某一条经过点Dn,求此时满足条件的正方形AnBnCnDn的边长.
相关试题

