【题目】阅读理解
(探究与发现)
在一次数学探究活动中,数学兴趣小组通过探究发现可以通过用“两数的差”来表示“数轴上两点间的距离”如图1中三条线段的长度可表示为:AB=4-2=2,CB=4-(-2)=6,DC=-2-(-4)=2,…结论:数轴上任意两点表示的数为分别a,b(b>a),则这两个点间的距离为b-a(即:用较大的数减去较小的数)

(理解与运用)
(1)如图2,数轴上E、F两点表示的数分别为-2,-5,试计算:EF=______,AF=______;
(2)在数轴上分别有三个点M,N,H三个点其中M表示的数为-18,点N表示的数为2018,已知点H为线段MN中点,若点H表示的数m,请你求出m的值;
(拓展与延伸)
(3)如图3,点A表示数x,点B表示-1,点C表示3x+8,且AB=![]() BC,求点A和点C分别表示什么数.
BC,求点A和点C分别表示什么数.
(4)在(3)条件下,在图3的数轴上是否存在满足条件的点D,使DA+DC=3DB,若存在,请直接写出点D表示的数;若不存在,请说明理由.
参考答案:
【答案】(1)3, 7;(2)m=1000;(3)点A表示数-2,点C表示的数是2;(4)点D所表示的数是-3或-![]() .
.
【解析】
(1)利用得出的结论直接计算即可;
(2)利用对称的性质列方程解答即可;
(3)根据图表示的数,利用BC=4AB,建立方程求得答案;
(4)设出点D表示的数,根据题意列出方程探讨得出答案即可.
(1)EF=-2-(-5)=3,FA=2-(-5)=7;
(2)m-(-18)=2018-m,
解得m=1000.
(3)![]()
解得:x=-2,
3x+8=2,
点A表示数-2,点C表示的数是2.
(4)存在,设点D表示的数为d.根据题意得:-2-d+2-d=3(-1-d)解得d=-3,
或d+2+2-d=3(d+1).解得![]() 故点D所表示的数是-3或
故点D所表示的数是-3或![]() .
.
故点D所表示的数是-3或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,将抛物线y=x2+2x+3绕着它与y轴的交点旋转180°,所得抛物线的解析式是( )
A.y=﹣(x+1)2+2
B.y=﹣(x﹣1)2+4
C.y=﹣(x﹣1)2+2
D.y=﹣(x+1)2+4 -
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,BC=a,AC=b,AB=c,若∠C=90°,如图(1),根据勾股定理,则a2+b2=c2,若△ABC不是直角三角形,如图(2)和图(3),请你类比勾股定理,试猜想a2+b2与c2的关系,并证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 ,
, ,
, ,
, 分别平分
分别平分 的外角
的外角 ,内角
,内角 ,外角
,外角 .以下结论:①
.以下结论:① ;②
;② ;③
;③ ;④
;④ 平分
平分 ;⑤
;⑤ .其中正确的结论有______________.(把正确结论序号填写在横线上)
.其中正确的结论有______________.(把正确结论序号填写在横线上)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A、B、C三点在数轴上,A表示的数为-10,B表示的数为14,点C为线段AB的中点,动点P在数轴上,且点P表示的数为m.
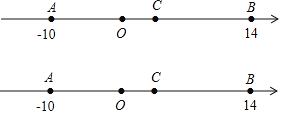
(1)求点C表示的数;
(2)点P从A点出发,沿射线AB向终点B运动,设BP的中点为M,用含m的整式表示线段MC的长.
(3)在(2)的条件下,当m为何值时,AP-CM=2PC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣1.25x2+4.25x+1与y轴交于A点,过点A的直线与抛物线交于另一点B,过点B作BC⊥x轴,垂足为点C(3,0)
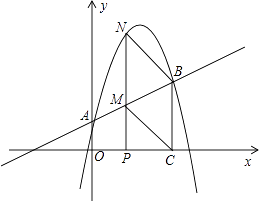
(1)求直线AB的函数关系式;
(2)动点P在线段OC上从原点出发以每秒一个单位的速度向C移动,过点P作PN⊥x轴,交直线AB于点M,交抛物线于点N.设点P移动的时间为t秒,MN的长度为s个单位,求s与t的函数关系式,并写出t的取值范围;
(3)设在(2)的条件下(不考虑点P与点O,点C重合的情况),连接CM,BN,当t为何值时,四边形BCMN为平行四边形?问对于所求的t值,平行四边形BCMN是否菱形?请说明理由. -
科目: 来源: 题型:
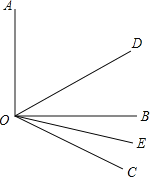
查看答案和解析>>【题目】已知,如图,∠AOB=90°,∠BOC=30°,OD、OE分别是∠AOC和∠BOC的平分线.
(1)求∠COD的度数;
(2)求∠DOE的度数;
(3)若把本题的条件改成∠AOB=α,∠BOC=β,那么∠DOE的度数是多少?
相关试题

