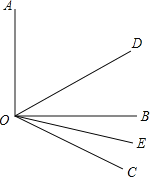
【题目】已知,如图,∠AOB=90°,∠BOC=30°,OD、OE分别是∠AOC和∠BOC的平分线.
(1)求∠COD的度数;
(2)求∠DOE的度数;
(3)若把本题的条件改成∠AOB=α,∠BOC=β,那么∠DOE的度数是多少?
参考答案:
【答案】(1)∠COD =60°;(2)∠DOE=45°;(3)∠DOE=![]() α.
α.
【解析】
(1)根据角平分线的定义即可得到结论;
(2)根据角平分线的定义可以得到![]() 然后根据∠DOE=∠COD-∠COE即可求解;
然后根据∠DOE=∠COD-∠COE即可求解;
(3)根据角平分线的定义可以得到![]() 然后根据∠DOE=∠COD-∠COE即可求解.
然后根据∠DOE=∠COD-∠COE即可求解.
(1)∵∠AOB=90°,∠BOC=30°,
∴∠AOC=120°,
∵OD平分∠AOC,
∴∠COD=![]() ∠AOC=60°;
∠AOC=60°;
(2)∵∠AOB=90°,∠BOC=30°,
∴∠AOC=∠AOB+∠BOC=90°+3,0°=120°
又∵OD,OE分别平分∠AOC和∠BOC,
∴∠COD=![]() ∠AOC=
∠AOC=![]() ×120°=60°,
×120°=60°,
∠COE=![]() ∠BOC=
∠BOC=![]() ×30°=15°,
×30°=15°,
∴∠DOE=∠COD-∠COE=60°-15°=45°;
(2)∵∠AOB=α,∠BOC=β,
∴∠AOC=∠AOB+∠BOC=α+β,
又∵OD,OE分别平分∠AOC和∠BOC,
∴∠COD=![]() ∠AOC=
∠AOC=![]() (α+β),
(α+β),
∠COE=![]() ∠BOC=
∠BOC=![]() β,
β,
∴∠DOE=∠COD-∠COE=![]() (α+β)-
(α+β)-![]() β=
β=![]() α+
α+![]() β-
β-![]() β=
β=![]() α.
α.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解
(探究与发现)
在一次数学探究活动中,数学兴趣小组通过探究发现可以通过用“两数的差”来表示“数轴上两点间的距离”如图1中三条线段的长度可表示为:AB=4-2=2,CB=4-(-2)=6,DC=-2-(-4)=2,…结论:数轴上任意两点表示的数为分别a,b(b>a),则这两个点间的距离为b-a(即:用较大的数减去较小的数)

(理解与运用)
(1)如图2,数轴上E、F两点表示的数分别为-2,-5,试计算:EF=______,AF=______;
(2)在数轴上分别有三个点M,N,H三个点其中M表示的数为-18,点N表示的数为2018,已知点H为线段MN中点,若点H表示的数m,请你求出m的值;
(拓展与延伸)
(3)如图3,点A表示数x,点B表示-1,点C表示3x+8,且AB=
 BC,求点A和点C分别表示什么数.
BC,求点A和点C分别表示什么数.(4)在(3)条件下,在图3的数轴上是否存在满足条件的点D,使DA+DC=3DB,若存在,请直接写出点D表示的数;若不存在,请说明理由.
-
科目: 来源: 题型:
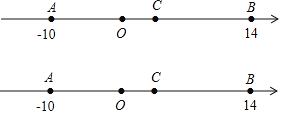
查看答案和解析>>【题目】如图,A、B、C三点在数轴上,A表示的数为-10,B表示的数为14,点C为线段AB的中点,动点P在数轴上,且点P表示的数为m.
(1)求点C表示的数;
(2)点P从A点出发,沿射线AB向终点B运动,设BP的中点为M,用含m的整式表示线段MC的长.
(3)在(2)的条件下,当m为何值时,AP-CM=2PC.
-
科目: 来源: 题型:
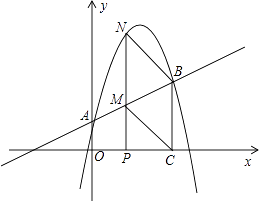
查看答案和解析>>【题目】如图,抛物线y=﹣1.25x2+4.25x+1与y轴交于A点,过点A的直线与抛物线交于另一点B,过点B作BC⊥x轴,垂足为点C(3,0)
(1)求直线AB的函数关系式;
(2)动点P在线段OC上从原点出发以每秒一个单位的速度向C移动,过点P作PN⊥x轴,交直线AB于点M,交抛物线于点N.设点P移动的时间为t秒,MN的长度为s个单位,求s与t的函数关系式,并写出t的取值范围;
(3)设在(2)的条件下(不考虑点P与点O,点C重合的情况),连接CM,BN,当t为何值时,四边形BCMN为平行四边形?问对于所求的t值,平行四边形BCMN是否菱形?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b的图象与x轴的交点坐标为(2,0),则下列说法:
①y随x的增大而减小;②b>0;③关于x的方程kx+b=0的解为x=2;④不等式kx+b>0的解集是x>2.
其中说法正确的有_________(把你认为说法正确的序号都填上).

-
科目: 来源: 题型:
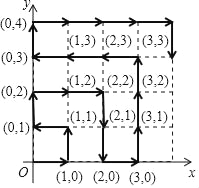
查看答案和解析>>【题目】如图,在平面直角坐标系中,有若干个横、纵坐标为整数的点,其顺序按图中“→”方向排列,从原点开始依次为(0,0),(1,0),(1,1),(0,1),(0,2),(1,2),(2,2),(2,1),(2,0)(3,0)…按此规律第200个点的坐标是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△OBC是直角三角形,OB与x轴正半轴重合,∠OBC=90°,且OB=1,BC=
 ,将△OBC绕原点O逆时针旋转60°再将其各边扩大为原来的m倍,使OB1=OC,得到△OB1C1 , 将△OB1C1绕原点O逆时针旋转60°再将其各边扩大为原来的m倍,使OB2=OC1 , 得到△OB2C2 , …,如此继续下去,得到△OB2017C2017 , 则m的值和点C2017的坐标是( )
,将△OBC绕原点O逆时针旋转60°再将其各边扩大为原来的m倍,使OB1=OC,得到△OB1C1 , 将△OB1C1绕原点O逆时针旋转60°再将其各边扩大为原来的m倍,使OB2=OC1 , 得到△OB2C2 , …,如此继续下去,得到△OB2017C2017 , 则m的值和点C2017的坐标是( )
A.2,(﹣22017 , 22017× )
)
B.2,(﹣22018 , 0)
C. , (﹣22017 , 22017×
, (﹣22017 , 22017×  )
)
D. , (﹣22018 , 0)
, (﹣22018 , 0)
相关试题

