【题目】如图,抛物线y=﹣1.25x2+4.25x+1与y轴交于A点,过点A的直线与抛物线交于另一点B,过点B作BC⊥x轴,垂足为点C(3,0)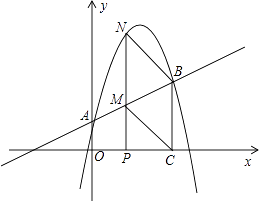
(1)求直线AB的函数关系式;
(2)动点P在线段OC上从原点出发以每秒一个单位的速度向C移动,过点P作PN⊥x轴,交直线AB于点M,交抛物线于点N.设点P移动的时间为t秒,MN的长度为s个单位,求s与t的函数关系式,并写出t的取值范围;
(3)设在(2)的条件下(不考虑点P与点O,点C重合的情况),连接CM,BN,当t为何值时,四边形BCMN为平行四边形?问对于所求的t值,平行四边形BCMN是否菱形?请说明理由.
参考答案:
【答案】
(1)解:∵当x=0时,y=1,∴A(0,1).
当x=3时,y=﹣ ![]() ×32+
×32+ ![]() ×3+1=2.5,∴B(3,2.5),
×3+1=2.5,∴B(3,2.5),
设直线AB的解析式为y=kx+b,
则: ![]() ,解得:
,解得: ![]() ,
,
∴直线AB的解析式为y= ![]() x+1
x+1
(2)解:∵动点P在线段OC上从原点出发以每秒一个单位的速度向C移动,点P移动的时间为t秒,
∴OP=1t=t,
∴P(t,0)(0≤t≤3),
∵过点P作PN⊥x轴,交直线AB于点M,交抛物线于点N,
∴M(t, ![]() t+1),N(t,﹣
t+1),N(t,﹣ ![]() t2+
t2+ ![]() t+1),
t+1),
∴s=MN=NP﹣MP=﹣ ![]() t2+
t2+ ![]() t+1﹣(
t+1﹣( ![]() t+1)=﹣
t+1)=﹣ ![]() t2+
t2+ ![]() t(0≤t≤3)
t(0≤t≤3)
(3)解:由题意,可知当MN=BC时,四边形BCMN为平行四边形,
此时,有﹣ ![]() t2+
t2+ ![]() t=
t= ![]() ,
,
解得t1=1,t2=2,
所以当t=1或2时,四边形BCMN为平行四边形.
①当t=1时,MP= ![]() ,NP=4,故MN=NP﹣MP=
,NP=4,故MN=NP﹣MP= ![]() ,
,
又在Rt△MPC中,MC= ![]() =
= ![]() ,故MN=MC,此时四边形BCMN为菱形;
,故MN=MC,此时四边形BCMN为菱形;
②当t=2时,MP=2,NP= ![]() ,故MN=NP﹣MP=
,故MN=NP﹣MP= ![]() ,
,
又在Rt△MPC中,MC= ![]() =
= ![]() ,故MN≠MC,此时四边形BCMN不是菱形.
,故MN≠MC,此时四边形BCMN不是菱形.
【解析】(1)将x=0、3分别代入函数解析式,求出对应的函数值,得到点A、B的坐标,利用待定系数法就可求出直线AB的解析式。
(2)根据题意得到OP=t,可得到点P的坐标,由PN⊥x轴,交直线AB于点M,交抛物线于点N,可得到点M、N的坐标,由s=MN=NP﹣MP,可求得s与t的函数解析式及t的取值范围。
(3)由题意知MN∥BC,因此当MN=BC时,四边形BCMN为平行四边形,建立方程,求解即可求得t的值;当t=1时,在Rt△MPC中,求出MC的长即可;②当t=2时,在Rt△MPC中求出MC即可判断平行四边形BCMN是否菱形。
【考点精析】通过灵活运用确定一次函数的表达式和抛物线与坐标轴的交点,掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 ,
, ,
, ,
, 分别平分
分别平分 的外角
的外角 ,内角
,内角 ,外角
,外角 .以下结论:①
.以下结论:① ;②
;② ;③
;③ ;④
;④ 平分
平分 ;⑤
;⑤ .其中正确的结论有______________.(把正确结论序号填写在横线上)
.其中正确的结论有______________.(把正确结论序号填写在横线上)
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解
(探究与发现)
在一次数学探究活动中,数学兴趣小组通过探究发现可以通过用“两数的差”来表示“数轴上两点间的距离”如图1中三条线段的长度可表示为:AB=4-2=2,CB=4-(-2)=6,DC=-2-(-4)=2,…结论:数轴上任意两点表示的数为分别a,b(b>a),则这两个点间的距离为b-a(即:用较大的数减去较小的数)

(理解与运用)
(1)如图2,数轴上E、F两点表示的数分别为-2,-5,试计算:EF=______,AF=______;
(2)在数轴上分别有三个点M,N,H三个点其中M表示的数为-18,点N表示的数为2018,已知点H为线段MN中点,若点H表示的数m,请你求出m的值;
(拓展与延伸)
(3)如图3,点A表示数x,点B表示-1,点C表示3x+8,且AB=
 BC,求点A和点C分别表示什么数.
BC,求点A和点C分别表示什么数.(4)在(3)条件下,在图3的数轴上是否存在满足条件的点D,使DA+DC=3DB,若存在,请直接写出点D表示的数;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A、B、C三点在数轴上,A表示的数为-10,B表示的数为14,点C为线段AB的中点,动点P在数轴上,且点P表示的数为m.
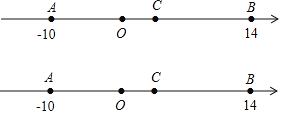
(1)求点C表示的数;
(2)点P从A点出发,沿射线AB向终点B运动,设BP的中点为M,用含m的整式表示线段MC的长.
(3)在(2)的条件下,当m为何值时,AP-CM=2PC.
-
科目: 来源: 题型:
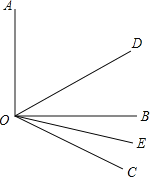
查看答案和解析>>【题目】已知,如图,∠AOB=90°,∠BOC=30°,OD、OE分别是∠AOC和∠BOC的平分线.
(1)求∠COD的度数;
(2)求∠DOE的度数;
(3)若把本题的条件改成∠AOB=α,∠BOC=β,那么∠DOE的度数是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b的图象与x轴的交点坐标为(2,0),则下列说法:
①y随x的增大而减小;②b>0;③关于x的方程kx+b=0的解为x=2;④不等式kx+b>0的解集是x>2.
其中说法正确的有_________(把你认为说法正确的序号都填上).

-
科目: 来源: 题型:
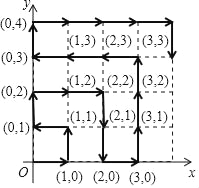
查看答案和解析>>【题目】如图,在平面直角坐标系中,有若干个横、纵坐标为整数的点,其顺序按图中“→”方向排列,从原点开始依次为(0,0),(1,0),(1,1),(0,1),(0,2),(1,2),(2,2),(2,1),(2,0)(3,0)…按此规律第200个点的坐标是_____.
相关试题

