【题目】△ABC中,BC=a,AC=b,AB=c,若∠C=90°,如图(1),根据勾股定理,则a2+b2=c2,若△ABC不是直角三角形,如图(2)和图(3),请你类比勾股定理,试猜想a2+b2与c2的关系,并证明你的结论.

参考答案:
【答案】见解析
【解析】
解:若△ABC为锐角三角形,则有a2+b2>c2,若△ABC为钝角三角形,∠C为钝角,则有a2+b2<c2.
证明:(1)当△ABC为锐角三角形时,过点A作AD⊥CB,垂足为D,设CD=x,则有DB=a-x.
根据勾股定理,得b2-x2=c2-(a-x)2,即b2-x2=c2-a2+2ax-x2.
∴a2+b2=c2+2ax.∵a>0,x>0,∴2ax>0,
∴a2+b2>c2.
(2)当△ABC为钝角三角形时,过B作BD⊥AC,交AC的延长线于点D,设CD=x,则BD2=a2-x2.根据勾股定理,得(b+x)2+(a2-x2)=c2,∴a2+b2+2bx=c2.
∵b>0,x>0,∴2bx>0,∴a2+b2<c2.

-
科目: 来源: 题型:
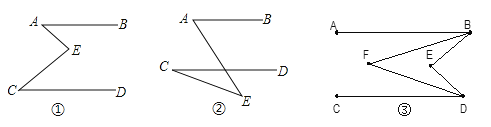
查看答案和解析>>【题目】(1)如图①、②,AB∥CD,你能说明∠A、∠E、∠C的关系吗?(请在图形下的横线上写出其关系并选一个进行说明)
(2)如图③若AB∥CD,BF平分∠ABE,DF平分∠CDE,∠BED=80,则∠BFD=________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一天,妈妈下班后从公司开车回家,途中想起忘了带第二天早上开早会的一个文件夹,于是打电话让办公室王阿姨马上从公司送来,同时妈妈也往回开,遇到王阿姨后停下说了几句话,接着继续开车回家.设妈妈从公司出发后所用时间为t,妈妈与家的距离为s.下面能反映s与t的函数关系的大致图象是( )
A.
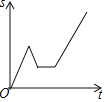 B.
B.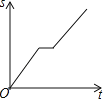
C.
 D.
D.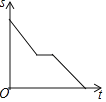
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知长方形相邻两边的长分别是xcm和3cm,设长方形的面积为ycm2.
(1)试写出长方形的面积y与x之间的关系式;
(2)利用(1)中的关系式,求当x=5cm时长方形的面积;
(3)当x的值由4cm变化到12cm时,长方形的面积由 cm2变化到 cm2.
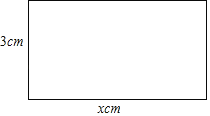
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某地某一天的气温随时间的变化而变化的图象,请根据图象回答:
(1)这一天什么时候气温最低?最低气温是多少?什么时候气温最高?最高气温是多少?
(2)求这一天的最大温差是多少?
(3)请你描述一下这一天气温随时间的变化情况.
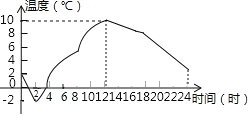
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将长方形纸片ABCD折叠,使点D与点B重合,点C落在点C'处,折痕为EF,若∠ABE=25°,则∠EFC'的度数为( )
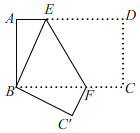
A.122.5°B.130°C.135°D.140°
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
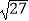 ﹣2cos30°+(
﹣2cos30°+(  )﹣2﹣|1﹣
)﹣2﹣|1﹣ 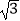 |.
|.
相关试题

