【题目】问题提出: 
(1)如图1,在正方形ABCD中,M是BC边(不含端点B、C)上任意一点,P是BC延长线上一点,N是∠DCP的平分线上一点.若∠AMN=90°,求证:AM=MN. 下面给出一种证明的思路,你可以按这一思路证明,也可以选择另外的方法证明.
证明:在边AB上截取AE=MC,连接ME.正方形ABCD中,∠B=∠BCD=90°,AB=BC.
∴∠NMC=180°﹣∠AMN﹣∠AMB=180°﹣∠B﹣∠AMB=∠MAB=∠MAE,即∠NMC=∠MAE.
(下面请你完成余下的证明过程)
(2)若将(1)中的“正方形ABCD”改为“正三角形ABC”(如图2),N是∠ACP的平分线上一点,则∠AMN=60°时,结论AM=MN是否还成立?请说明理由.
(3)若将(1)中的“正方形ABCD”改为“正n边形ABCD…X,请你作出猜想:当∠AMN=时,结论AM=MN仍然成立.(直接写出答案,不需要证明)
参考答案:
【答案】
(1)解:证明:如图1,

在边AB上截取AE=MC,连接ME.
∵正方形ABCD中,∠B=∠BCD=90°,AB=BC,
∴∠NMC=180°﹣∠AMN﹣∠AMB=180°﹣∠B﹣∠AMB=∠MAB=∠MAE,BE=AB﹣AE=BC﹣MC=BM,
∴∠BEM=45°,
∴∠AEM=135°,
∵N是∠DCP的平分线上一点,
∴∠NCP=45°,
∴∠MCN=135°,
在△AEM与△MCN中,
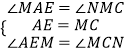 ,
,
∴△AEM≌△MCN(ASA),
∴AM=MN
(2)解:结论AM=MN还成立,
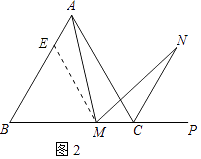
证明:如图2,在边AB上截取AE=MC,连接ME.
在正△ABC中,∠B=∠BCA=60°,AB=BC,
∴∠NMC=180°﹣∠AMN﹣∠AMB=180°﹣∠B﹣∠AMB=∠MAE,BE=AB﹣AE=BC﹣MC=BM,
∴∠BEM=60°,
∴∠AEM=120°,
∵N是∠ACP的平分线上一点,
∴∠ACN=60°,
∴∠MCN=120°,
在△AEM与△MCN中,
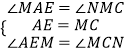 ,
,
∴△AEM≌△MCN(ASA),
∴AM=MN
(3)![]()
【解析】解决问题:(3)解:∵当AM=MN时,△AEM≌△MCN, 此时∠NMC=∠MAE,
又∵∠AMN=180°﹣∠NMC﹣∠AMB,∠MAE=180°﹣∠BAM﹣∠AMB,
∴∠AMN=∠B= ![]() ,
,
∴将(1)中的“正方形ABCD”改为“正n边形ABCD…X,则
当∠AMN= ![]() 时,结论AM=MN仍然成立.
时,结论AM=MN仍然成立.
所以答案是: ![]()
【考点精析】认真审题,首先需要了解等边三角形的性质(等边三角形的三个角都相等并且每个角都是60°),还要掌握正方形的性质(正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若∠A的两边与∠B的两边分别平行,且∠A的度数比∠B的度数的3倍少40°,则∠B的度数为( )
A. 20° B. 55° C. 20°或55° D. 75°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,∠B=90°,DE∥AB,DE交BC于E,交AC于F,DE=BC,∠CDE=∠ACB=30°.
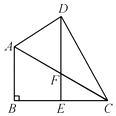
(1)若AB=4,求CD的长.
(2)判断△FCD的形状,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中错误的个数是( )
(1)过一点有且只有一条直线与已知直线平行
(2)过一点有且只有一条直线与已知直线垂直
(3)在同一平面内,两条直线的位置关系只有相交、平行两种
(4)不相交的两条直线叫做平行线
(5)有公共顶点且有一条公共边的两个角互为邻补角。
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题是真命题的是( )
A. 同位角相等 B. 有且只有一条直线与已知直线垂直
C. 垂线段最短 D. 直线外一点到这条直线的垂线段,叫做点到直线的距离
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数 y=ax2+a与 y=
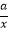 ( a≠0)在同一坐标系中的图象可能是图中的( )
( a≠0)在同一坐标系中的图象可能是图中的( )
A.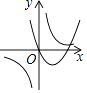
B.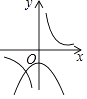
C.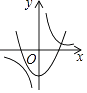
D.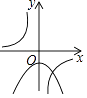
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A、B分别表示的数是6、-12、M、N、P为数轴上三个动点,它们同时都向右运动。点M从点A出发,速度为每秒2个单位长度,点N从点B出发,速度为点M的3倍,点P从原点出发,速度为每秒1个单位长度。
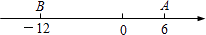
(1)当运动3秒时,点M、N、P分别表示的数是、、;
(2)求运动多少秒时,点P到点M、N的距离相等?
相关试题

