搜索
【题目】函数 y=ax2+a与 y= 
（ a≠0）在同一坐标系中的图象可能是图中的（ ）
A.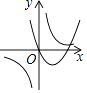
B.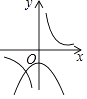
C.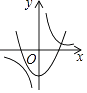
D.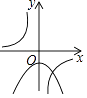
参考答案：
【答案】D
【解析】解：当a＞0时，二次函数y=ax2+a的图象开口向上、对称轴为y轴、顶点在y轴正半轴，反比例函数y= 
的图象在第一、三象限； 当a＜0时，二次函数y=ax2+a的图象开口向下、对称轴为y轴、顶点在y轴负半轴，反比例函数y= 的图象在第二、四象限．
对照四个选项可知D正确．
故选D．
【考点精析】解答此题的关键在于理解反比例函数的图象的相关知识，掌握反比例函数的图像属于双曲线．反比例函数的图象既是轴对称图形又是中心对称图形．有两条对称轴：直线y=x和 y=-x．对称中心是：原点，以及对二次函数图象以及系数a、b、c的关系的理解，了解二次函数y=ax2+bx+c中，a、b、c的含义：a表示开口方向：a>0时，抛物线开口向上; a<0时，抛物线开口向下b与对称轴有关：对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标：（0，c）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列说法中错误的个数是( )
(1)过一点有且只有一条直线与已知直线平行
(2)过一点有且只有一条直线与已知直线垂直
(3)在同一平面内，两条直线的位置关系只有相交、平行两种
(4)不相交的两条直线叫做平行线
(5)有公共顶点且有一条公共边的两个角互为邻补角。
A. 1个 B. 2个 C. 3个 D. 4个
-
科目： 来源： 题型：
查看答案和解析>>【题目】问题提出：
（1）如图1，在正方形ABCD中，M是BC边（不含端点B、C）上任意一点，P是BC延长线上一点，N是∠DCP的平分线上一点．若∠AMN=90°，求证：AM=MN． 下面给出一种证明的思路，你可以按这一思路证明，也可以选择另外的方法证明．
证明：在边AB上截取AE=MC，连接ME．正方形ABCD中，∠B=∠BCD=90°，AB=BC．
∴∠NMC=180°﹣∠AMN﹣∠AMB=180°﹣∠B﹣∠AMB=∠MAB=∠MAE，即∠NMC=∠MAE．
（下面请你完成余下的证明过程）
（2）若将（1）中的“正方形ABCD”改为“正三角形ABC”（如图2），N是∠ACP的平分线上一点，则∠AMN=60°时，结论AM=MN是否还成立？请说明理由．
（3）若将（1）中的“正方形ABCD”改为“正n边形ABCD…X，请你作出猜想：当∠AMN=时，结论AM=MN仍然成立．（直接写出答案，不需要证明） -
科目： 来源： 题型：
查看答案和解析>>【题目】下列命题是真命题的是( )
A. 同位角相等 B. 有且只有一条直线与已知直线垂直
C. 垂线段最短 D. 直线外一点到这条直线的垂线段，叫做点到直线的距离
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点A、B分别表示的数是6、-12、M、N、P为数轴上三个动点，它们同时都向右运动。点M从点A出发，速度为每秒2个单位长度，点N从点B出发，速度为点M的3倍，点P从原点出发，速度为每秒1个单位长度。
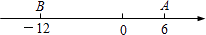
（1）当运动3秒时，点M、N、P分别表示的数是、、；
（2）求运动多少秒时，点P到点M、N的距离相等？ -
科目： 来源： 题型：
查看答案和解析>>【题目】钟面角是指时钟的时针与分针所成的角．如图，图①、图②、图③三个钟面上的时刻分别记录了某中学的早晨上课时间7：30、中午放学时间11：50、下午放学时间17：00．
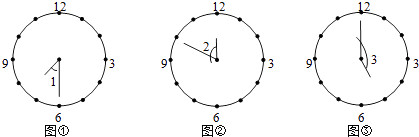
（1）分别写出图中钟面角的度数：∠1=°、∠2=°、∠3=°；
（2）在某个整点，钟面角可能会等于90°，写出可能的一个时刻为；
（3）请运用一元一次方程的知识解决问题：钟面上，在7：30～8：00之间，钟面角等于90°的时刻是多少？ -
科目： 来源： 题型：
查看答案和解析>>【题目】下列运算中，正确的是（ ）
A.5a﹣2a=3
B.（x+2y）2=x2+4y2
C.x8÷x4=x2
D.（2a）3=8a3
相关试题
