【题目】(1)阅读思考:
小迪在学习过程中,发现“数轴上两点间的距离”可以用“表示这两点数的差”来表示,探索过程如下:
如图1所示,线段AB,BC,CD的长度可表示为:AB=3=4﹣1,BC=5=4﹣(﹣1),CD=3=(﹣1)﹣(﹣4),于是他归纳出这样的结论:如果点A表示的数为a,点B表示的数为b,当b>a时,AB=b﹣a(较大数﹣较小数).

(2)尝试应用:
①如图2所示,计算:OE= ,EF= ;
②把一条数轴在数m处对折,使表示﹣19和2019两数的点恰好互相重合,则m= ;

(3)问题解决:
①如图3所示,点P表示数x,点M表示数﹣2,点N表示数2x+8,且MN=4PM,求出点P和点N分别表示的数;
②在上述①的条件下,是否存在点Q,使PQ+QN=3QM?若存在,请直接写出点Q所表示的数;若不存在,请说明理由.

参考答案:
【答案】(2)①5,8;②1000;(3)①点 P表示的数为﹣3,点 N表示的数为2;②﹣5或﹣![]()
【解析】
(2)尝试应用:①利用得出的结论直接计算即可;
②利用对称的性质列方程解答即可;
(3)问题解决:①根据图表示的数,利用MN=4PM,建立方程求得答案;
②设出点D表示的数,根据题意列出方程探讨得出答案即可.
(2)尝试应用:
①OE=0-(-5)=5,EF=3-(-5)=8,
②m﹣(﹣19)=2019﹣m,
解得m=1000;
故答案为:5,8,1000;
(3)问题解决:
①∵MN=2x+8﹣(﹣2),PM=﹣2﹣x,
∵MN=4PM,
∴2x+10=4(﹣2﹣x),
∴x=﹣3,2x+8=2
∴点 P表示的数为﹣3,点 N表示的数为2;
②存在,分析题意可知Q只能在P点左侧或者在MN之间,设点Q表示的数为a,
当Q在P点左侧时:根据题意得:﹣3﹣a+2﹣a=3(﹣2﹣a)解得a=﹣5;当点Q在MN之间时:a+3+2﹣a=3(a+2),
解得a=﹣![]() ;
;
故点Q表示的数为﹣5或﹣![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,连接BD,在BD的延长线上取一点E,在DB的延长线上取一点F,使BF=DE,连接AF,CE.
求证:AF∥CE.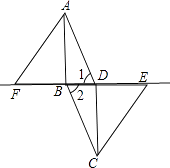
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A,B为定点,定直线l//AB,P是l上一动点.点M,N分别为PA,PB的中点,对于下列各值:
①线段MN的长;
②△PAB的周长;
③△PMN的面积;
④直线MN,AB之间的距离;
⑤∠APB的大小.
其中会随点P的移动而变化的是( )

A. ②③ B. ②⑤ C. ①③④ D. ④⑤
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,直角∠EPF的顶点和正方形ABCD的顶点C重合,两直角边PE,PF分别和AB,AD所在的直线交于点E和F.易得△PBE≌△PDF,故结论“PE=PF”成立;

(1)如图2,若点P在正方形ABCD的对角线AC上,其他条件不变,(1)中的结论是否仍然成立?说明理由;
(2)如图(3)将(2)中正方形ABCD改为矩形ABCD其他条件不变,若AB=m,BC=n,直接写出 的值.
的值. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知矩形OABC的三个顶点A(0,10),B(8,10),C(8,0),过O、C两点的抛物线y=ax2+bx+c与线段AB交于点D,沿直线CD折叠矩形OABC的一边BC,使点B落在OA边上的点E处.
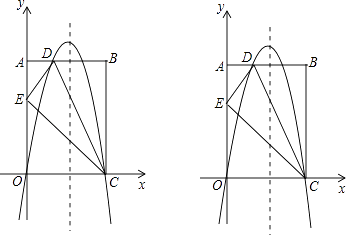
(1)求AD的长及抛物线的解析式;
(2)一动点P从点E出发,沿EC以每秒2个单位长的速度向点C运动,同时动点Q从点C出发,沿CO以每秒1个单位长的速度向点O运动,当点P运动到点C时,两点同时停止运动.设运动时间为t秒.请问当t为何值时,以P、Q、C为顶点的三角形是等腰三角形?
(3)若点N在抛物线对称轴上,点M在抛物线上,是否存在这样的点M与点N,使以M、N、C、E为顶点四边形是平行四边形?若存在,请直接写出点M与点N的坐标(不写求解过程);若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校实行学案式教学,需印制若干份教学学案.印刷厂有,甲、乙两种收费方式,除按印数收取印刷费外,甲种方式还需收取制版费而乙种不需要,两种印刷方式的费用y(元)与印刷份数x(份)之间的关系如图所示.
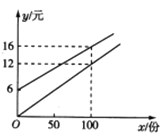
(1)填空:甲种收费方式的函数关系式是__________,乙种收费方式的函数关系式是__________.
(2)该校某年级每次需印制100~450(含100和450)份学案,选择哪种印刷方式较合算.
-
科目: 来源: 题型:
查看答案和解析>>【题目】民族图案是数学文化中的一块瑰宝.下列图案中,既不是中心对称图形也不是轴对称图形的是( )
A.
B.
C.
D.
相关试题

