【题目】已知O为直线AB上一点,射线OD、OC、OE位于直线AB上方,OD在OE的左侧,∠AOC=120°,∠DOE=50°,设∠BOE=![]()
(1)若射线OE在∠BOC的内部(如图所示):
①若![]() =43°,求∠COD的度数;
=43°,求∠COD的度数;
②当∠AOD=3∠COE时,求∠COD的度数;
(2)若射线OE恰为图中某一个角(小于180°)的角平分线,试求![]() 的值.
的值.

参考答案:
【答案】(1)①33°②15°
(2)n的值为30°或50°或110°或120°
【解析】
(1)①根据已知条件,可先求出∠COE,再根据角的差求出∠COD
②分两种情况讨论:当OD在∠BOC之间时;OD在∠AOC内的情况
(2)分四种情况讨论:当OE分别是∠BOC、∠BOD、∠COD、∠COA的角平分线时,根据角平分线的性质分别求出即可
(1)①∵∠BOC=180°∠AOC,∠AOC=120°
∴∠BOC=180°120°=60°
∵∠COE=∠BOC∠BOE,∠BOE=n=43°
∠COD=∠DOE∠COE,∠DOE=50°
∴∠COD=50°(60°43°)=33°
②当∠DOE在∠BOC之间时,设∠COD=x,则由题意可得:120+x=3(50+x)无解;
当OD在∠AOC之间时,设∠COD=x,则由题意可得120-x=3(50-x)解得x=15°
所以当∠AOD=3∠COE时,∠COD=15°
(2)如图: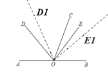
当OE1平分∠BOC时,
∵∠AOC=120°
∴∠BOC=180°120°=60°
∴n=∠BOE1= ∠BOC=30°;
如图: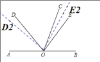
当OE2平分∠BOD2时,
n=∠BOE2=∠D2OE=50°;
如图: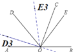
当OE3平分∠COD3时,
∵∠E3OC=∠D3OE3=50°,∠BOC=180°∠AOC=180°120°=60°
∴n=∠BOE3=∠BOC+∠E3OC=60°+50°=110°;
如图: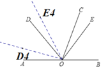
当OE4平分∠AOC时,
∵∠COE4= ∠AOC= ×120°=60°
∠BOC=180°∠AOC=180°120°=60°
∴n=∠BOE4=∠BOC+∠COE4=60°+60°=120°
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着某市教育改革的不断深入,素质教育的全面推进,中学生利用假期参加社会实践的调查越来越多,一位同学在A公司实习调查时,计划部给了他一份实习作业;在下述条件下,规划下个月的产量,若公司生产部有工人200名,每个工人的月劳动时间不超过196h,每个工人生产一件产品需用2h;本月将剩余原料60吨,下个月准备购进300吨,每件产品需原料20kg;经市场调查,预计下个月市场对这种产品的需求量不少于16000件,公司准备充分保证市场要求,你能和这位同学一同规划出下个月的产量范围吗?(设下个月产量为x件)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形OABC的边OA,OC分别在x轴、y轴上,点B在第一象限,点D在边BC上,且∠AOD=30°,四边形OA′B′D与四边形OABD关于直线OD对称(点A′和A,B′和B分别对应).若AB=1,反比例函数y=
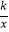 (k≠0)的图象恰好经过点A′,B,则k的值为 .
(k≠0)的图象恰好经过点A′,B,则k的值为 . 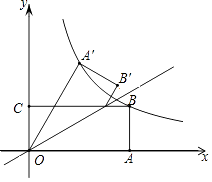
-
科目: 来源: 题型:
查看答案和解析>>【题目】一副含
 和
和 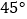 角的三角板
角的三角板  和
和 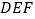 叠合在一起,边
叠合在一起,边 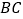 与
与 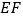 重合,
重合, 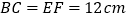 (如图1),点
(如图1),点 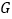 为边
为边 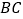
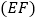 的中点,边
的中点,边 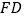 与
与 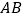 相交于点
相交于点  .现将三角板
.现将三角板 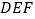 绕点
绕点 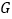 按顺时针方向旋转(如图2),在
按顺时针方向旋转(如图2),在 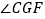 从
从  到
到 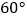 的变化过程中,点
的变化过程中,点  相应移动的路径长为 . (结果保留根号)
相应移动的路径长为 . (结果保留根号)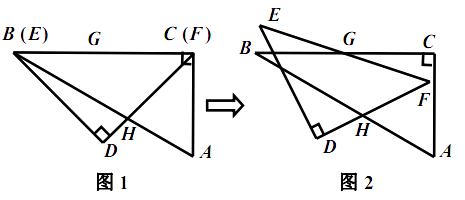
-
科目: 来源: 题型:
查看答案和解析>>【题目】南水北调工程中线自2014年12月正式通水以来,沿线多座大中城市受益,河南、河北、北京及天津四个省(市)的水资源紧张态势得到缓解,有效促进了地下水资源的涵养和恢复.若与上年同期相比,北京地下水的水位下降记为负,回升记为正,记录从2013年底以来,北京地下水水位的变化得到下表:
时间
2013年底
2014年底
2015年底
2016年底
2017年底
2018年9月底
地下水位与上年同比变化量(单位:
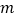 )
)-0.25
-1.14
-0.09
+0.52
+0.26
+2.12
以下关于2013年以来北京地下水水位的说法不正确的是( )
A. 从2014年底开始,北京地下水水位的下降趋势得到缓解
B. 从2015年底到2016年底,北京地下水水位首次回升
C. 2013年以来,每年年底的地下水位与上年同比的回升量最大的是2018年
D. 2018年9月底的地下水位低于2012年底的地下水水位
-
科目: 来源: 题型:
查看答案和解析>>【题目】线段
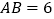 ,在直线
,在直线 上截取线段
上截取线段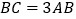 ,
, 为线段
为线段 的中点,
的中点, 为线段
为线段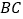 的中点,那么线段
的中点,那么线段 的长为______.
的长为______. -
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC在平面直角坐标系中的位置如图所示.
(1)作出△ABC关于
 轴对称的△A1B1C1,并写出△A1B1C1各顶点的坐标;
轴对称的△A1B1C1,并写出△A1B1C1各顶点的坐标;(2)将△ABC向右平移6个单位,作出平移后的△A2B2C2,并写出△A2B2C2各顶点的坐标;
(3)观察△A1B1C和△A2B2C2,它们是否关于某直线对称?若是,请用实线条画出对称轴。

相关试题

