【题目】线段![]() ,在直线
,在直线![]() 上截取线段
上截取线段![]() ,
,![]() 为线段
为线段![]() 的中点,
的中点,![]() 为线段
为线段![]() 的中点,那么线段
的中点,那么线段![]() 的长为______.
的长为______.
参考答案:
【答案】6或12
【解析】
分类讨论:C在线段AB的延长线上,C在线段AB的反向延长线上,根据BC=3AB,可得BC的长,根据中点的性质,可得BD,BE的长,根据线段的和差,可得答案.
解:C在线段AB的延长线上,如图1:
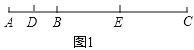
∵AB=6,BC=3AB,
∴BC=18,
∵D为线段AB的中点,E为线段BC的中点,
BD=![]() AB=3,BE=
AB=3,BE=![]() BC=9,
BC=9,
DE=BD+BE=9+3=12;
C在线段AB的反向延长线上,如图2:
![]()
∵AB=6,BC=3AB,
∴BC=18,
∵D为线段AB的中点,E为线段BC的中点,
BD=![]() AB=3,BE=
AB=3,BE=![]() BC=9,
BC=9,
DE=BD-BE=9-3=6.
故线段DE的长为6或12.
故答案为:6或12.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一副含
 和
和 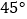 角的三角板
角的三角板  和
和 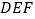 叠合在一起,边
叠合在一起,边 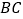 与
与 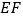 重合,
重合, 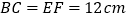 (如图1),点
(如图1),点 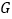 为边
为边 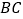
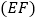 的中点,边
的中点,边 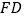 与
与 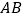 相交于点
相交于点  .现将三角板
.现将三角板 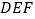 绕点
绕点 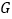 按顺时针方向旋转(如图2),在
按顺时针方向旋转(如图2),在 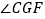 从
从  到
到 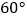 的变化过程中,点
的变化过程中,点  相应移动的路径长为 . (结果保留根号)
相应移动的路径长为 . (结果保留根号)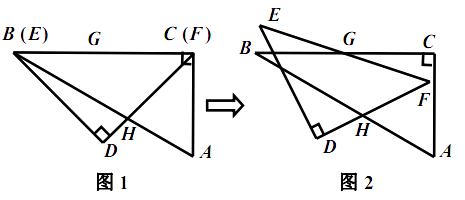
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知O为直线AB上一点,射线OD、OC、OE位于直线AB上方,OD在OE的左侧,∠AOC=120°,∠DOE=50°,设∠BOE=

(1)若射线OE在∠BOC的内部(如图所示):
①若
 =43°,求∠COD的度数;
=43°,求∠COD的度数;②当∠AOD=3∠COE时,求∠COD的度数;
(2)若射线OE恰为图中某一个角(小于180°)的角平分线,试求
 的值.
的值.
-
科目: 来源: 题型:
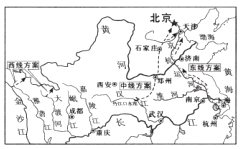
查看答案和解析>>【题目】南水北调工程中线自2014年12月正式通水以来,沿线多座大中城市受益,河南、河北、北京及天津四个省(市)的水资源紧张态势得到缓解,有效促进了地下水资源的涵养和恢复.若与上年同期相比,北京地下水的水位下降记为负,回升记为正,记录从2013年底以来,北京地下水水位的变化得到下表:
时间
2013年底
2014年底
2015年底
2016年底
2017年底
2018年9月底
地下水位与上年同比变化量(单位:
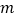 )
)-0.25
-1.14
-0.09
+0.52
+0.26
+2.12
以下关于2013年以来北京地下水水位的说法不正确的是( )
A. 从2014年底开始,北京地下水水位的下降趋势得到缓解
B. 从2015年底到2016年底,北京地下水水位首次回升
C. 2013年以来,每年年底的地下水位与上年同比的回升量最大的是2018年
D. 2018年9月底的地下水位低于2012年底的地下水水位
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC在平面直角坐标系中的位置如图所示.
(1)作出△ABC关于
 轴对称的△A1B1C1,并写出△A1B1C1各顶点的坐标;
轴对称的△A1B1C1,并写出△A1B1C1各顶点的坐标;(2)将△ABC向右平移6个单位,作出平移后的△A2B2C2,并写出△A2B2C2各顶点的坐标;
(3)观察△A1B1C和△A2B2C2,它们是否关于某直线对称?若是,请用实线条画出对称轴。

-
科目: 来源: 题型:
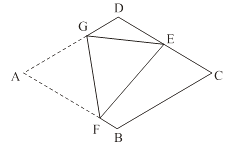
查看答案和解析>>【题目】如图,在菱形纸片ABCD中,AB=2,∠A=60°,将菱形纸片翻折,使点A落在CD的中点E处,折痕为FG,点F、G分别在边AB、AD上.则cos∠EFG的值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】有个均匀的正十二面体的骰子,其中1个面标有“1”,2个面标有“2”,3个面标有“3”,2个面标有“4”,1个面标有“5”,其余面标有“6”,将这个骰子掷出后:
(1)掷出“6”朝上的可能性有多大?
(2)哪些数字朝上的可能性一样大?
(3)哪些数字朝上的可能性最大?
相关试题

