【题目】如图,矩形OABC的边OA,OC分别在x轴、y轴上,点B在第一象限,点D在边BC上,且∠AOD=30°,四边形OA′B′D与四边形OABD关于直线OD对称(点A′和A,B′和B分别对应).若AB=1,反比例函数y= ![]() (k≠0)的图象恰好经过点A′,B,则k的值为 .
(k≠0)的图象恰好经过点A′,B,则k的值为 . 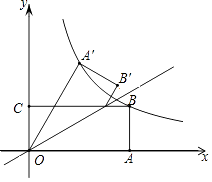
参考答案:
【答案】![]()
【解析】解:∵四边形ABCO是矩形,AB=1,
∴设B(m,1),
∴OA=BC=m,
∵四边形OA′B′D与四边形OABD关于直线OD对称,
∴OA′=OA=m,∠A′OD=∠AOD=30°,
∴∠A′OA=60°,
过A′作A′E⊥OA于E,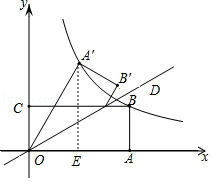
∴OE= ![]() m,A′E=
m,A′E= ![]() m,
m,
∴A′( ![]() m,
m, ![]() m),
m),
∵反比例函数y= ![]() (k≠0)的图象恰好经过点A′,B,
(k≠0)的图象恰好经过点A′,B,
∴ ![]() m
m ![]() m=m,
m=m,
∴m= ![]() ,
,
∴k= ![]() .
.
所以答案是: ![]() .
.
【考点精析】解答此题的关键在于理解矩形的性质的相关知识,掌握矩形的四个角都是直角,矩形的对角线相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一条道路上,甲车从A地到B地,乙车从B地到A地,乙先出发,图中的折线段表示甲、乙两车之间的距离y(千米)与行驶时间x(小时)的函数关系的图象.下列说法错误的是( )

A.乙先出发的时间为0.5小时
B.甲的速度是80千米/小时
C.甲出发0.5小时后两车相遇
D.甲到B地比乙到A地早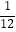 小时
小时 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点(﹣1,y1),(4,y2)在一次函数y=3x﹣2的图象上,则y1 , y2 , 0的大小关系是( )
A.0<y1<y2
B.y1<0<y2
C.y1<y2<0
D.y2<0<y1 -
科目: 来源: 题型:
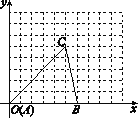
查看答案和解析>>【题目】如图,在平面直角坐标系中,三角形ABC的顶点坐标分别是A(0,0),B(6,0),C(5,5).
(1)求三角形ABC的面积;
(2)如果三角形ABC的三个顶点的纵坐标不变,横坐标增加3个单位长度,得到三角形A1B1C1,试在图中画出三角形A1B1C1,并写出点A1,B1,C1的坐标;
(3)(2)中三角形A1B1C1与三角形ABC的大小、形状有什么关系?
-
科目: 来源: 题型:
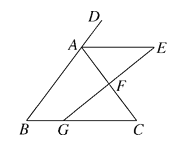
查看答案和解析>>【题目】如图,在△ABC中,已知点D在线段AB的反向延长线上,过AC的中点F作线段GE交∠DAC的平分线于E,交BC于G,且AE∥BC.
(1)求证:△ABC是等腰三角形;
(2)若AE=8,AB=10,GC=2BG,求△ABC的周长.
-
科目: 来源: 题型:
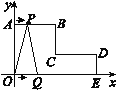
查看答案和解析>>【题目】如图,在平面直角坐标系中,AB∥CD∥x轴,BC∥DE∥y轴,且AB=CD=4 cm,OA=5 cm,DE=2 cm,动点P从点A出发,以每秒1 cm的速度,沿ABC路线向点C运动;动点Q从点O出发,以每秒2 cm的速度,沿OED路线向点D运动.若P,Q两点同时出发,其中一点到达终点时,运动停止.
(1)直接写出B,C,D三个点的坐标;
(2)当P,Q两点出发3 s时,求三角形PQC的面积;
(3)设两点运动的时间为t s,用含t的式子表示运动过程中三角形OPQ的面积.
-
科目: 来源: 题型:
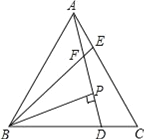
查看答案和解析>>【题目】如图,已知△ABC为等边三角形,AE=CD,AD、BE相交于点F.
(1)求证:△ABE≌△CAD;
(2)若BP⊥AD于点P,PF=9,EF=3,求AD的长.
相关试题

