【题目】如图,![]() 的顶点都在边长为1的正方形方格纸的格点上,将
的顶点都在边长为1的正方形方格纸的格点上,将![]() 向左平移2格,再向上平移4格.
向左平移2格,再向上平移4格.
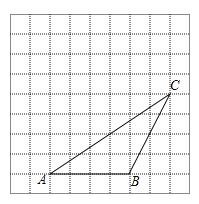
(1)在图中画出平移后的三角形![]() ;
;
(2)在图中画出三角形![]() 的高
的高![]() 、中线
、中线![]() ;
;
(3)图中线段![]() 与
与![]() 的关系是_____;
的关系是_____;
(4)![]() 的面积是_____.
的面积是_____.
参考答案:
【答案】(1)见解析;(2)见解析;(3)平行且相等;(4)8.
【解析】
(1)根据图形平移的性质画出平移后的△A′B′C′即可;
(2)找出线段A′C′的中点E′,连接B′E′,再过点C′向A′B′所在的直线作垂线,垂足为D′即可;
(3)根据图形平移的性质即可得出结论;
(4)直接根据三角形的面积公式即可得出结论.
(1)如图所示;
(2)如图所示;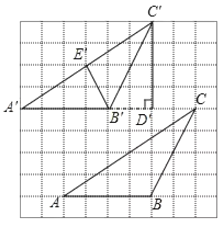
(3)∵△A′B′C′由△ABC平移而成,
∴线段AB与A′B′平行且相等.
故答案为:平行且相等;
(4)S△ABC=![]() ×4×4=8.故答案为:8.
×4×4=8.故答案为:8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】复习课中,教师给出关于x的函数y=2kx2-(4k+1)x-k+1(k是实数).教师:请独立思考,并把探索发现的与该函数有关的结论(性质)写到黑板上.学生思考后,黑板上出现了一些结论,教师作为活动一员,又补充一些结论,并从中选出如下四条:
①存在函数,其图象经过(1,0)点;
②存在函数,该函数的函数值y始终随x的增大而减小;
③函数图象有可能经过两个象限;
④若函数有最大值,则最大值必为正数,若函数有最小值,则最小值必为负数.
其中正确的结论有 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,AB∥CD∥x轴,BC∥DE∥y轴,且AB=CD=4cm,OA=5cm,DE=2cm,动点P从点A出发,沿A→B→C路线运动到点C停止;动点Q从点O出发,沿O→E→D→C路线运动到点C停止;若P、Q两点同时出发,且点P的运动速度为1cm/s,点Q的运动速度为2cm/s.
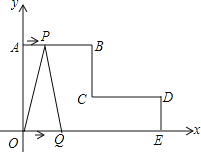
(1)直接写出B、C、D三个点的坐标;
(2)当P、Q两点出发
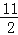 s时,试求△PQC的面积;
s时,试求△PQC的面积;(3)设两点运动的时间为t s,用t的式子表示运动过程中△OPQ的面积S.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一元一次方程的根是一元一次不等式组的解,则称该一元一次方程为该不等式组的关联方程.
(1)在方程①3x-1=0,②
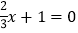 ③x-(3x+1)=-5 中,不等组
③x-(3x+1)=-5 中,不等组 的关联方程是________
的关联方程是________ (2)若不等式组
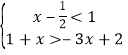 的一个关联方程的根是整数, 则这个关联方程可以是________(写出一个即可)
的一个关联方程的根是整数, 则这个关联方程可以是________(写出一个即可) (3)若方程 3-x=2x,3+x=
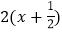 都是关于 x 的不等式组
都是关于 x 的不等式组  的关联方程,直接写出 m 的取值范围.
的关联方程,直接写出 m 的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为
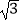 的正方形ABCD中,动点F,E分别以相同的速度从D,C两点同时出发向C和B运动(任何一个点到达即停止),在运动过程中,则线段CP的最小值为 .
的正方形ABCD中,动点F,E分别以相同的速度从D,C两点同时出发向C和B运动(任何一个点到达即停止),在运动过程中,则线段CP的最小值为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】
 中,
中, ,点
,点 分别是边
分别是边 上的点,点
上的点,点 是一动点,令
是一动点,令 ,
, ,
, .
.(1)若点
 在线段
在线段 上,如图①所示,且
上,如图①所示,且 ,则
,则 _____
_____ ;
;(2)若点
 在边
在边 上运动,如图②所示,则
上运动,如图②所示,则 、
、 、
、 之间的关系为______;
之间的关系为______;(3)如图③,若点
 在斜边
在斜边 的延长线上运动
的延长线上运动 ,请写出
,请写出 、
、 、
、 之间的关系式,并说明理由.
之间的关系式,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“五一”期间,小明一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游。
 [来
[来根据以上信息,解答下列问题:
(1)设租车时间为
 小时,租用甲公司的车所需费用为
小时,租用甲公司的车所需费用为 元,租用乙公司的车所需费用为
元,租用乙公司的车所需费用为 元,分别求出
元,分别求出 ,
, 关于
关于 的函数表达式;
的函数表达式;(2)请你帮助小明计算并选择哪个出游方案合算。
相关试题

