【题目】如图,在平面直角坐标系中,AB∥CD∥x轴,BC∥DE∥y轴,且AB=CD=4cm,OA=5cm,DE=2cm,动点P从点A出发,沿A→B→C路线运动到点C停止;动点Q从点O出发,沿O→E→D→C路线运动到点C停止;若P、Q两点同时出发,且点P的运动速度为1cm/s,点Q的运动速度为2cm/s.
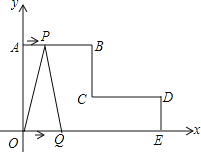
(1)直接写出B、C、D三个点的坐标;
(2)当P、Q两点出发![]() s时,试求△PQC的面积;
s时,试求△PQC的面积;
(3)设两点运动的时间为t s,用t的式子表示运动过程中△OPQ的面积S.
参考答案:
【答案】(1)B(4,5),C(4,2),D(8,2);(2)![]() ;(3)S=
;(3)S=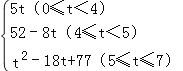 .
.
【解析】
试题分析:(1)根据平面直角坐标系写出各点的坐标即可;
(2)先求出点P、Q的坐标,再求出CP、CQ,然后根据三角形的面积公式列式计算即可得解;
(3)分①0≤t<4时点P在AB上,点Q在OE上,利用三角形面积公式列式即可;
②4≤t<5时,点P在BC上,点Q在DE上,过点P作PM∥CD交DE的延长线于M,根据S△OPQ=S梯形OPMB﹣S△PMQ﹣S△OEQ,列式整理即可;
③5≤t≤7时,点P在BC上,点Q在CD上,过点P作PF∥CD,过点Q作QF∥OA交PF于F,交OE于G,S△OPQ=S梯形OPFG﹣S△PFQ﹣S△OGQ,列式整理即可得解.
解:(1)B(4,5),C(4,2),D(8,2);
(2)当t=![]() s时,点P运动的路程为
s时,点P运动的路程为![]() ,
,
点Q运动的路程为![]() ×2=11,
×2=11,
所以,P(4,![]() ),Q(7,2),
),Q(7,2),
∴CP=![]() ,CQ=3,
,CQ=3,
∴S△CPQ=![]() CPCQ=
CPCQ=![]() ×
×![]() ×3=
×3=![]() ;
;
(3)由题意得,
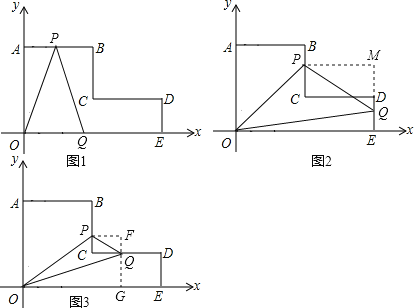
①当0≤t<4时,(如图1)OA=5,OQ=2t,
S△OPQ=![]() OQOA=
OQOA=![]() ×2t×5=5t;
×2t×5=5t;
②当4≤t<5时,(如图2)OE=8,EM=9﹣t,PM=4,MQ=17﹣3t,EQ=2t﹣8,
S△OPQ=S梯形OPMB﹣S△PMQ﹣S△OEQ,
=![]() (4+8)×(9﹣t)﹣
(4+8)×(9﹣t)﹣![]() ×4(17﹣3t)﹣
×4(17﹣3t)﹣![]() ×8(2t﹣8),
×8(2t﹣8),
=52﹣8t;
③当5≤t≤7时,(如图3)PF=14﹣2t,FQ=7﹣t,QG=2,OG=18﹣2t,FG=9﹣t,
S△OPQ=S梯形OPFG﹣S△PFQ﹣S△OGQ,
=![]() ×(14﹣2t+18﹣2t)×(9﹣t)﹣
×(14﹣2t+18﹣2t)×(9﹣t)﹣![]() ×(14﹣2t)(7﹣t)﹣
×(14﹣2t)(7﹣t)﹣![]() (18﹣2t)×2,
(18﹣2t)×2,
=t2﹣18t+77,
综上所述,S=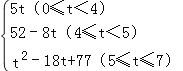 .
.
-
科目: 来源: 题型:
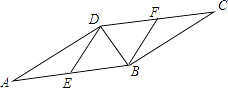
查看答案和解析>>【题目】如图,在ABCD中,BD是对角线,且DB⊥BC,E、F分别为边AB、CD的中点.求证:四边形DEBF是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图1,M是定长线段AB上一定点,C、D两点分别从M、B出发以1cm/s、3cm/s的速度沿直线BA向左运动,运动方向如箭头所示(C在线段AM上,D在线段BM上)
(1)若AB=10cm,当点C、D运动了2s,求AC+MD的值.
(2)若点C、D运动时,总有MD=3AC,直接填空:AM= AB.
(3)在(2)的条件下,N是直线AB上一点,且AN-BN=MN,求
 的值.
的值.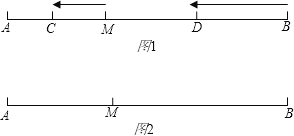
-
科目: 来源: 题型:
查看答案和解析>>【题目】复习课中,教师给出关于x的函数y=2kx2-(4k+1)x-k+1(k是实数).教师:请独立思考,并把探索发现的与该函数有关的结论(性质)写到黑板上.学生思考后,黑板上出现了一些结论,教师作为活动一员,又补充一些结论,并从中选出如下四条:
①存在函数,其图象经过(1,0)点;
②存在函数,该函数的函数值y始终随x的增大而减小;
③函数图象有可能经过两个象限;
④若函数有最大值,则最大值必为正数,若函数有最小值,则最小值必为负数.
其中正确的结论有 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如果一元一次方程的根是一元一次不等式组的解,则称该一元一次方程为该不等式组的关联方程.
(1)在方程①3x-1=0,②
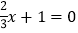 ③x-(3x+1)=-5 中,不等组
③x-(3x+1)=-5 中,不等组 的关联方程是________
的关联方程是________ (2)若不等式组
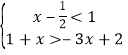 的一个关联方程的根是整数, 则这个关联方程可以是________(写出一个即可)
的一个关联方程的根是整数, 则这个关联方程可以是________(写出一个即可) (3)若方程 3-x=2x,3+x=
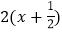 都是关于 x 的不等式组
都是关于 x 的不等式组  的关联方程,直接写出 m 的取值范围.
的关联方程,直接写出 m 的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
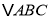 的顶点都在边长为1的正方形方格纸的格点上,将
的顶点都在边长为1的正方形方格纸的格点上,将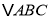 向左平移2格,再向上平移4格.
向左平移2格,再向上平移4格.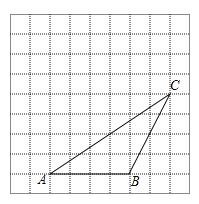
(1)在图中画出平移后的三角形
 ;
;(2)在图中画出三角形
 的高
的高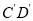 、中线
、中线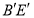 ;
;(3)图中线段
 与
与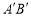 的关系是_____;
的关系是_____;(4)
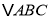 的面积是_____.
的面积是_____. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为
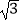 的正方形ABCD中,动点F,E分别以相同的速度从D,C两点同时出发向C和B运动(任何一个点到达即停止),在运动过程中,则线段CP的最小值为 .
的正方形ABCD中,动点F,E分别以相同的速度从D,C两点同时出发向C和B运动(任何一个点到达即停止),在运动过程中,则线段CP的最小值为 . 
相关试题

