【题目】【探究证明】
(1)某班数学课题学习小组对矩形内两条互相垂直的线段与矩形两邻边的数量关系进行探究,提出下列问题,请你给出证明.
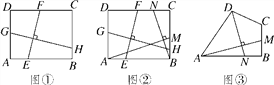
如图①,在矩形ABCD中,EF⊥GH,EF分别交AB,CD于点E,F,GH分别交AD,BC于点G,H.求证: ![]() ;
;
【结论应用】
(2)如图②,在满足(1)的条件下,又AM⊥BN,点M,N分别在边BC,CD上,若![]() ,则
,则![]() 的值为 ;
的值为 ;
【联系拓展】
(3)如图③,四边形ABCD中,∠ABC=90°,AB=AD=10,BC=CD=5,AM⊥DN,点M,N分别在边BC,AB上,求![]() 的值.
的值.
参考答案:
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析: (1)过点A作AP∥EF,交CD于P,过点B作BQ∥GH,交AD于Q,如图1,易证AP=EF,GH=BQ,△PDA∽△QAB,然后运用相似三角形的性质就可解决问题,
(2)只需运用(1)中的结论,就可得到![]() ,就可解决问题,
,就可解决问题,
(3)过点D作平行于AB的直线,交过点A平行于BC的直线于R,交BC的延长线于S,如图3,易证四边形ABSR是矩形,由(1)中的结论可得=.设SC=x,DS=y,则AR=BS=5+x,RD=10﹣y,在Rt△CSD中根据勾股定理可得![]() ①,在Rt△ARD中根据勾股定理可得
①,在Rt△ARD中根据勾股定理可得![]() +
+![]() =100②,解①②就可求出x,即可得到AR,问题得以解决.
=100②,解①②就可求出x,即可得到AR,问题得以解决.
试题解析: (1)过点A作AP∥EF,交CD于P,过点B作BQ∥GH,交AD于Q,如图1,
∵四边形ABCD是矩形,
∴AB∥DC,AD∥BC,
∴四边形AEFP,四边形BHGQ都是平行四边形,
∴AP=EF,GH=BQ,
又∵GH⊥EF,
∴AP⊥BQ,
∴∠QAT+∠AQT=90°,
∵四边形ABCD是矩形,
∴∠DAB=∠D=90°,
∴∠DAP+∠DPA=90°,
∴∠AQT=∠DPA,
∴△PDA∽△QAB,
∴![]() ,
,
∴![]() ,
,
(2)如图2,
∵EF⊥GH,AM⊥BN,
∴由(1)中的结论可得![]() ,
,![]() ,
,
∴![]()
故答案为: ![]() ,
,
(2)过点D作平行于AB的直线,交过点A平行于BC的直线于R,交BC的延长线于S,如图3,则四边形ABSR是平行四边形,
∵∠ABC=90°,
∴ABSR是矩形,
∴∠R=∠S=90°,RS=AB=10,AR=BS,
∵AM⊥DN,
∴由(1)中的结论可得![]() ,
,
设SC=x,DS=y,则AR=BS=5+x,RD=10﹣y,
∴在Rt△CSD中,x2+y2=25①,
在Rt△ARD中,(5+x)2+(10﹣y)2=100②,
由②﹣①得x=2y﹣5③,
解方程组![]() 得
得
![]() (舍去),或
(舍去),或![]() ,
,
∴AR=5+x=8,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y1=kx+b和反比例函数y2=
 的图象交于A、B两点.
的图象交于A、B两点.
(1)求一次函数y1=kx+b和反比例函数y2=
 的解析式;
的解析式;(2)观察图象写出y1<y2时,x的取值范围为 ;
(3)求△OAB的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,M是△ABC的边BC的中点,AN平分
 ,BN
,BN AN于点N,延长BN交AC于点D,已知AB=10,AC=16.
AN于点N,延长BN交AC于点D,已知AB=10,AC=16.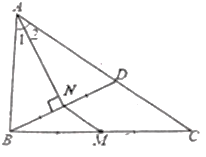
(1)求证:BN=DN;
(2)求MN的长.
-
科目: 来源: 题型:
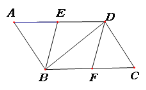
查看答案和解析>>【题目】如图,在平行四边形ABCD中,点E、F分别是AD、BC的中点,分别连接BE、DF、BD.
(1)求证:△AEB≌△CFD;
(2)当△ABD满足什么条件时,四边形EBFD是菱形,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司组织退休职工组团前往某景点游览参观,参加人员共70人.旅游景点规定:①门票每人60元,无优惠;②上山游览必须乘坐景点安排的观光车游览,观光车有小型车和中型车两类,分别可供4名和11名乘客乘坐;且小型车每辆收费60元,中型车每人收费10元.若70人正好坐满每辆车且参观游览的总费用不超过5000元,问景点安排的小型车和中型车各多少辆?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在我市“青山绿水”行动中,某社区计划对面积为
 的区域进行绿化,经投标由甲、乙两个工程队来完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍,如果两队各自独立完成面积为
的区域进行绿化,经投标由甲、乙两个工程队来完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍,如果两队各自独立完成面积为 区域的绿化时,甲队比乙队少用6天.
区域的绿化时,甲队比乙队少用6天.(1)求甲、乙两工程队每天各能完成多少面积的绿化;
(2)若甲队每天绿化费用是1.2万元,乙队每天绿化费用为0.5万元,社区要使这次绿化的总费用不超过40万元,则至少应安排乙工程队绿化多少天?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a≠0,a、b、c为常数)的图象如图所示,下列5个结论:①abc<0;②b<a+c;③4a+2b+c>0;④c<4b;⑤a+b<k(ka+b)(k为常数,且k≠1).其中正确的结论有( )
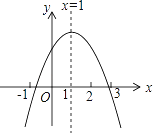
A. 2个 B. 3个 C. 4个 D. 5个
相关试题

