【题目】某公司组织退休职工组团前往某景点游览参观,参加人员共70人.旅游景点规定:①门票每人60元,无优惠;②上山游览必须乘坐景点安排的观光车游览,观光车有小型车和中型车两类,分别可供4名和11名乘客乘坐;且小型车每辆收费60元,中型车每人收费10元.若70人正好坐满每辆车且参观游览的总费用不超过5000元,问景点安排的小型车和中型车各多少辆?
参考答案:
【答案】小型车租1辆,中型车租6辆.
【解析】设小型车租x辆,中型车租y辆,先根据“共有70名职工”作为相等关系列出x,y的方程,再根据“70人正好坐满每辆车且参观游览的总费用不超过5000元”作为不等关系列不等式,求x,y的整数解即可.注意求得的解要代入实际问题中检验.
设小型车租x辆,中型车租y辆,则有:
![]() ,
,
将4x+11y=70变形为:4x=70﹣11y,代入70×60+60x+11y×10≤5000,可得:
70×60+15(70﹣11y)+11y×10≤5000,
解得:y≥![]() ,
,
又∵x=![]() ≥0,
≥0,
∴y≤![]() ,
,
故y=5,6.
当y=5时,x=![]() (不合题意舍去).
(不合题意舍去).
当y=6时,x=1.
答:小型车租1辆,中型车租6辆.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校九年级(1)班所有学生参加2010年初中毕业生升学体育测试,根据测试评分标准,将他们的成绩进行统计后分为A、B、C、D四等,并绘制成如图所示的条形统计图和扇形统计图(未完成),请结合图中所给信息解答下列问题:

(1)九年级(1)班参加体育测试的学生有 人;
(2)将条形统计图补充完整;
(3)在扇形统计图中,等级B部分所占的百分比是 ,等级C对应的圆心角的度数为 ;
(4)若该校九年级学生共有850人参加体育测试,估计达到A级和B级的学生共有 人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列网格中建立平面直角坐标系如图,每个小正方形的边长均为1个单位长度.已知A(1,1)、B(3,4)和C(4,2).
(1)在图中标出点A、B、C.
(2)将点C向下平移3个单位到D点,将点A先向左平移3个单位,再向下平移1个单位到E点,在图中标出D点和E点.
(3)求△EBD的面积S△EBD.

-
科目: 来源: 题型:
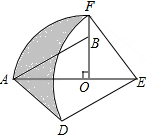
查看答案和解析>>【题目】如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=2,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以O,E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分面积是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂现有甲种原料3600kg,乙种原料2410kg,计划利用这两种原料生产A,B两种产品共500件,产品每月均能全部售出.已知生产一件A产品需要甲原料9kg和乙原料3kg;生产一件B种产品需甲种原料4kg和乙种原料8kg.
(1)设生产x件A种产品,写出x应满足的不等式组.
(2)问一共有几种符合要求的生产方案?并列举出来.
(3)若有两种销售定价方案,第一种定价方案可使A产品每件获得利润1.15万元,B产品每件获得利润1.25万元;第二种定价方案可使A和B产品每件都获得利润1.2万元;在上述生产方案中哪种定价方案盈利最多?(请用数据说明)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC和△DCE均是等腰三角形,CA=CB,CD=CE,∠BCA=∠DCE.

(1)求证:BD=AE;
(2)若∠BAC=70°,求∠BPE的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,在△ABC中,∠ACB=2∠B,∠C=90°,AD为∠BAC的平分线交BC于D,求证:AB=AC+CD.(提示:在AB上截取AE=AC,连接DE)



(2)如图2,当∠C≠90°时,其他条件不变,线段AB、AC、CD又有怎样的数量关系,直接写出结果,不需要证明.
(3)如图3,当∠ACB≠90°,∠ACB=2∠B ,AD为△ABC的外角∠CAF的平分线,交BC的延长线于点D,则线段 AB、AC、CD又有怎样的数量关系?写出你的猜想,并加以证明.
相关试题

