【题目】我们知道:任意一个有理数与无理数的和为无理数,任意一个不为零的有理数与一个无理数的积为无理数,而零与无理数的积为零.由此可得:如果ax+b=0,其中a、b为有理数,x为无理数,那么a=0且b=0.
运用上述知识,解决下列问题:
(1)如果(a+2) ![]() -b+3=0,其中a、b为有理数,那么a= , b=;
-b+3=0,其中a、b为有理数,那么a= , b=;
(2)如果2b-a-(a+b-4) ![]() =5,其中a、b为有理数,求3a+2b的平方根.
=5,其中a、b为有理数,求3a+2b的平方根.
参考答案:
【答案】
(1)-2,3
(2)解:已知等式整理得:2b-a-(a+b-4) ![]() -5=0,
-5=0,
∴ ![]() ,
,
解得: ![]() ,
,
则3a+2b=9,9的平方根为±3
【解析】(1)根据a、b为有理数,如果(a+2) 2 -b+3=0,那么a+2=0且-b+3=0,从而得出a,b的值;
(2)已知等式右边化为0,根据a,b为有理数,求出a,b的值,即可确定出3a+2b的平方根。
【考点精析】本题主要考查了实数的运算的相关知识点,需要掌握先算乘方、开方,再算乘除,最后算加减,如果有括号,先算括号里面的,若没有括号,在同一级运算中,要从左到右进行运算才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各项是真命题的是( )
A. 从直线外一点到已知直线的垂线段叫做这点到直线的距离
B. 过一点有且只有一条直线与已知直线平行
C. 有公共顶点且相等的两个角是对顶角
D. 同一平面内,不重合的两条直线的位置关系只有相交和平行两种
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C,E,F,B在同一直线上,点A,D在BC异侧,AB∥CD,AE=DF,∠A=∠D.
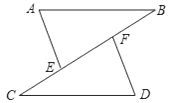
(1)求证:AB=CD;
(2)若AB=CF,∠B=40°,求∠D的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:(x+2)(x-6)+16
-
科目: 来源: 题型:
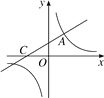
查看答案和解析>>【题目】如图,直线y=
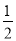 x+2与双曲线y=
x+2与双曲线y=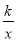 相交于点A(m,3),与x轴交于点C.
相交于点A(m,3),与x轴交于点C.(1)求双曲线的解析式;
(2)点P在x轴上,如果△ACP的面积为3,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数y=ax2+
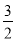 x+c的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),连接AB、AC.
x+c的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),连接AB、AC.(1)请直接写出二次函数y=ax2+
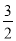 x+c的表达式;
x+c的表达式;(2)判断△ABC的形状,并说明理由;
(3)若点N在x轴上运动,当以点A、N、C为顶点的三角形是等腰三角形时,请直接写出此时点N的坐标;
(4)若点N在线段BC上运动(不与点B、C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求此时点N的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】若2m-4与3m-1是同一个数的平方根,则m的值是( )
A. 3B. 1或3C. 1D. 1或-3
相关试题

