【题目】如图,点C,E,F,B在同一直线上,点A,D在BC异侧,AB∥CD,AE=DF,∠A=∠D.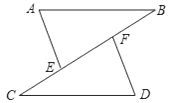
(1)求证:AB=CD;
(2)若AB=CF,∠B=40°,求∠D的度数.
参考答案:
【答案】
(1)证明:∵AB∥CD,
∴∠B=∠C,
在△ABE和△CDF中,
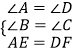 ,
,
∴△ABE≌△CDF(AAS),
∴AB=CD;
(2)解:∵△ABE≌△CDF,
∴AB=CD,BE=CF,∠B=∠C,
∵∠B=40°,
∴∠C=40°
∵AB=CF,
∴CF=CD,
∴∠D=∠CFE= ![]() (180°-40°)=70°
(180°-40°)=70°
【解析】(1)由平行线的性质得出∠B=∠C,然后由AAS判断出△ABE≌△CDF,根据三角形全等对应边相等得出结论;
(2)根据全等三角形的性质得出AB=CD,BE=CF,∠B=∠C,,然后根据等边对等角得出∠D=∠CFE,从而得出结论。
-
科目: 来源: 题型:
查看答案和解析>>【题目】对八(2)班的一次考试成绩进行统计,已知75.5~85.5分这一组的频数是9,频率是0.2,那么该班级的人数是 人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)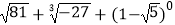 ;
;
(2)(-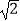 )2+|1-
)2+|1- 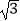 |+(-
|+(-  )-1 .
)-1 . -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各项是真命题的是( )
A. 从直线外一点到已知直线的垂线段叫做这点到直线的距离
B. 过一点有且只有一条直线与已知直线平行
C. 有公共顶点且相等的两个角是对顶角
D. 同一平面内,不重合的两条直线的位置关系只有相交和平行两种
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:(x+2)(x-6)+16
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道:任意一个有理数与无理数的和为无理数,任意一个不为零的有理数与一个无理数的积为无理数,而零与无理数的积为零.由此可得:如果ax+b=0,其中a、b为有理数,x为无理数,那么a=0且b=0.
运用上述知识,解决下列问题:
(1)如果(a+2)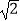 -b+3=0,其中a、b为有理数,那么a= , b=;
-b+3=0,其中a、b为有理数,那么a= , b=;
(2)如果2b-a-(a+b-4)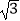 =5,其中a、b为有理数,求3a+2b的平方根.
=5,其中a、b为有理数,求3a+2b的平方根. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=
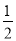 x+2与双曲线y=
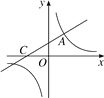
x+2与双曲线y=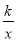 相交于点A(m,3),与x轴交于点C.
相交于点A(m,3),与x轴交于点C.(1)求双曲线的解析式;
(2)点P在x轴上,如果△ACP的面积为3,求点P的坐标.
相关试题

