【题目】如图,![]() 中,
中,![]() ,
,![]() 于
于![]() ,
,![]() 平分
平分![]() ,且
,且![]() 于
于![]() ,与
,与![]() 相交于点
相交于点![]() ,
,![]() 是
是![]() 边的中点,连接
边的中点,连接![]() 与
与![]() 相交于点
相交于点![]() ,下列结论正确的有( )个
,下列结论正确的有( )个
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 是等腰三角形;⑤
是等腰三角形;⑤![]() .
.

A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
参考答案:
【答案】B
【解析】
只要证明△BDF≌△CDA,△BAC是等腰三角形,∠DGF=∠DFG=67.5°,即可判断①②③④正确,作GM⊥BD于M,只要证明GH<DG即可判断⑤错误.
∵CD⊥AB,BE⊥AC,
∴∠BDC=∠ADC=∠AEB=90°,
∴∠A+∠ABE=90°,∠ABE+∠DFB=90°,
∴∠A=∠DFB,
∵∠ABC=45°,∠BDC=90°,
∴∠DCB=90°45°=45°=∠DBC,
∴BD=DC,
在△BDF和△CDA中
 ,
,
∴△BDF≌△CDA(AAS),
∴BF=AC,故①正确.
∵∠ABE=∠EBC=22.5°,BE⊥AC,
∴∠A=∠BCA=67.5°,故③正确,
∴BA=BC,
∵BE⊥AC,
∴AE=EC=![]() AC=
AC=![]() BF,故②正确,
BF,故②正确,
∵BE平分∠ABC,∠ABC=45°,
∴∠ABE=∠CBE=22.5°,
∵∠BDF=∠BHG=90°,
∴∠BGH=∠BFD=67.5°,
∴∠DGF=∠DFG=67.5°,
∴DG=DF,故④正确.
作GM⊥AB于M.
∵∠GBM=∠GBH,GH⊥BC,
∴GH=GM<DG,
∴S△DGB>S△GHB,
∵S△ABE=S△BCE,
∴S四边形ADGE<S四边形GHCE.故⑤错误,
∴①②③④正确,
故选:B.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知排球场的长度OD为18 m,位于球场中线处球网的高度AB为2.4 m,一队员站在点O处发球,排球从点O的正上方1.6 m的C点向正前方飞出,当排球运行至离点O的水平距离OE为6 m时,到达最高点G建立如图所示的平面直角坐标系
(1) 当球上升的最大高度为3.4 m时,对方距离球网0.4 m的点F处有一队员,他起跳后的最大高度为3.1 m,问这次她是否可以拦网成功?请通过计算说明
(2) 若队员发球既要过球网,又不出边界,问排球飞行的最大高度h的取值范围是多少?(排球压线属于没出界)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
 在
在 的内部,点
的内部,点 关于
关于 、
、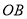 的对称点分别为
的对称点分别为 、
、 ,连接
,连接 交
交 、
、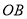 于点
于点 、
、 ,若
,若 ,则下列结论错误的是( )
,则下列结论错误的是( )
A.
 B.
B.
C.
 D.
D. 垂直平分
垂直平分
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC是等边三角形
(1) 如图1,点E在线段AB上,点D在射线CB上,且ED=EC,将△BCE绕点C顺时针旋转60°至△ACF,连接EF,猜想线段AB、DB、AF之间的数量关系
(2) 点E在线段BA的延长线上,其他条件与(1)中的一致,请在图2上将图形补充完整,并猜想证明线段AB、DB、AF之间的数量关系

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A、B两点,点A在点B左侧,点B的坐标为(1,0),C(0,-3)
(1) 求抛物线的解析式;
(2) 若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值.
(3) 若点E在x轴上,点P在抛物线上,是否存在以A、C、E、P为顶点且以AC为一边的平行四边形?若存在,求点P的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,
, 平分
平分 交边
交边 于点
于点 ,
, 分别是
分别是 ,
, 上的点,连结
上的点,连结 ,
, .若
.若 ,
, ,
, 则
则 的最小值是__________.
的最小值是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,点
,点 、
、 、
、 分别在
分别在 、
、 、
、 边上,且
边上,且 ,
, .
.
(1)求证:
 是等腰三角形;
是等腰三角形;(2)当
 时,求
时,求 的度数;
的度数;(3)当
 为多少度时,
为多少度时, ?请说明理由.
?请说明理由.
相关试题

