【题目】如图,已知排球场的长度OD为18 m,位于球场中线处球网的高度AB为2.4 m,一队员站在点O处发球,排球从点O的正上方1.6 m的C点向正前方飞出,当排球运行至离点O的水平距离OE为6 m时,到达最高点G建立如图所示的平面直角坐标系
(1) 当球上升的最大高度为3.4 m时,对方距离球网0.4 m的点F处有一队员,他起跳后的最大高度为3.1 m,问这次她是否可以拦网成功?请通过计算说明
(2) 若队员发球既要过球网,又不出边界,问排球飞行的最大高度h的取值范围是多少?(排球压线属于没出界)

参考答案:
【答案】(1)可以拦网成功,理由见解析;(2)h≥3.025
【解析】
(1)根据此时抛物线顶点坐标为(6,3.4),设解析式为y=a(x﹣6)2+3.4,再将点C坐标代入即可求得;由解析式求得x=9.4时y的值,与他起跳后的最大高度为3.1米比较即可得;
(2)设抛物线解析式为y=a(x﹣6)2+h,将点C坐标代入得到用h表示a的式子,再根据球既要过球网,又不出边界即x=9时,y>2.4且x=18时,y≤0得出关于h的不等式组,解之即可得.
(1)根据题意知此时抛物线的顶点G的坐标为(6,3.4),
设抛物线解析式为y=a(x﹣6)2+3.4,
将点C(0,1.6)代入,得:36a+3.4=1.6,
解得:a=﹣![]() ,
,
∴排球飞行的高度y与水平距离x的函数关系式为y=﹣![]() (x﹣6)2+
(x﹣6)2+![]() ;
;
由题意当x=9.5时,y=﹣![]() (9.4﹣6)2+
(9.4﹣6)2+![]() ≈2.8<3.1,
≈2.8<3.1,
故这次她可以拦网成功;
(3)设抛物线解析式为y=a(x﹣6)2+h,
将点C(0,1.6)代入,得:36a+h=1.6,即a=![]() ,
,
∴此时抛物线解析式为y=![]() (x﹣6)2+h,
(x﹣6)2+h,
根据题意,得: ,
,
解得:h≥3.025,
答:排球飞行的最大高度h的取值范围是h≥3.025.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB=90°,OM平分∠AOB,将直角三角板的顶点P在射线OM上移动,两直角边分别与OA、OB相交于点C、D,问PC与PD相等吗?试说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(
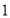 ),在四边形
),在四边形 中,
中, ,
, ,
, ,
, ,
, 分别是
分别是 ,
, 上的点,且
上的点,且 .探究图中线段
.探究图中线段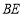 ,
, ,
, 之间的数量关系.小王同学探究此问题的方法是,延长
之间的数量关系.小王同学探究此问题的方法是,延长 到点
到点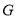 ,使
,使 ,连接
,连接 ,先证明
,先证明 ≌
≌ ,再证明
,再证明 ≌
≌ ,可得出结论,他的结论应该是__________.
,可得出结论,他的结论应该是__________.如图(
 ),若在四边形
),若在四边形 中,
中, ,
, ,
, ,
, 分别是
分别是 ,
, 上的点,且
上的点,且 ,上述结论是否仍然成立,并说明理由.
,上述结论是否仍然成立,并说明理由.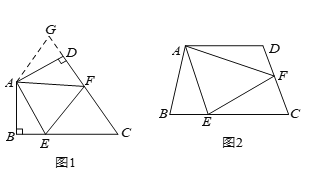
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中BC边上的垂直平分线DE与∠BAC得平分线交于点E,EF⊥AB交AB的延长线于点F,EG⊥AC交于点G.
求证:(1)BF=CG;(2)AF=
 (AB+AC).
(AB+AC).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
 在
在 的内部,点
的内部,点 关于
关于 、
、 的对称点分别为
的对称点分别为 、
、 ,连接
,连接 交
交 、
、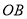 于点
于点 、
、 ,若
,若 ,则下列结论错误的是( )
,则下列结论错误的是( )
A.
 B.
B.
C.
 D.
D. 垂直平分
垂直平分
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC是等边三角形
(1) 如图1,点E在线段AB上,点D在射线CB上,且ED=EC,将△BCE绕点C顺时针旋转60°至△ACF,连接EF,猜想线段AB、DB、AF之间的数量关系
(2) 点E在线段BA的延长线上,其他条件与(1)中的一致,请在图2上将图形补充完整,并猜想证明线段AB、DB、AF之间的数量关系

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 中,
中, ,
, 于
于 ,
, 平分
平分 ,且
,且 于
于 ,与
,与 相交于点
相交于点 ,
, 是
是 边的中点,连接
边的中点,连接 与
与 相交于点
相交于点 ,下列结论正确的有( )个
,下列结论正确的有( )个①
 ;②
;② ;③
;③ ;④
;④ 是等腰三角形;⑤
是等腰三角形;⑤ .
.
A.
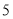 个B.
个B. 个C.
个C. 个D.
个D. 个
个
相关试题

