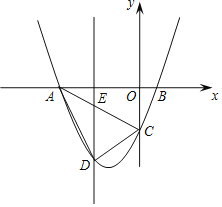
【题目】已知如图,抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A、B两点,点A在点B左侧,点B的坐标为(1,0),C(0,-3)
(1) 求抛物线的解析式;
(2) 若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值.
(3) 若点E在x轴上,点P在抛物线上,是否存在以A、C、E、P为顶点且以AC为一边的平行四边形?若存在,求点P的坐标;若不存在,请说明理由.

参考答案:
【答案】(1)![]() ;(2)S△ACD的最大值为
;(2)S△ACD的最大值为![]() ;(3)见解析.
;(3)见解析.
【解析】
(1)将B、C的坐标代入抛物线中,求出待定系数的值,即可得出抛物线的解析式.
(2)根据A、C的坐标,易求得直线AC的解析式.由于AB、OC都是定值,则△ABC的面积不变,若四边形ABCD面积最大,则△ADC的面积最大;过点D作DE∥y轴交AC于E,则E(m,﹣![]() m﹣3),可得到当△ADC面积有最大值时,四边形ABCD的面积最大值,然后列出四边形的面积与m的函数关系式,利用配方法可求得此时m的取值范围;
m﹣3),可得到当△ADC面积有最大值时,四边形ABCD的面积最大值,然后列出四边形的面积与m的函数关系式,利用配方法可求得此时m的取值范围;
(3)本题应分情况讨论:①过C作x轴的平行线,与抛物线的交点符合P点的要求,此时P、C的纵坐标相同,代入抛物线的解析式中即可求出P点坐标;②将AC平移,令C点落在x轴(即E点)、A点落在抛物线(即P点)上;可根据平行四边形的性质,得出P点纵坐标(P、C纵坐标的绝对值相等),代入抛物线的解析式中即可求得P点坐标.
解:(1)将点B、C的坐标代入抛物线的解析式得:![]() ,
,
解得:a=![]() ,c=﹣3.
,c=﹣3.
∴抛物线的解析式为y=![]() x2+
x2+![]() x﹣3
x﹣3
(2)令y=0,则![]() x2+
x2+![]() x﹣3=0,解得x1=1,x2=﹣4
x﹣3=0,解得x1=1,x2=﹣4
∴A(﹣4,0)、B(1,0)
令x=0,则y=﹣3
∴C(0,﹣3)
∴S△ABC=![]() ×5×3=
×5×3=![]()
设D(m,![]() m2+
m2+![]() m﹣3)
m﹣3)
过点D作DE∥y轴交AC于E.直线AC的解析式为y=﹣![]() x﹣3,则E(m,﹣
x﹣3,则E(m,﹣![]() m﹣3)
m﹣3)
DE=﹣![]() m﹣3﹣(
m﹣3﹣(![]() m2+
m2+![]() m﹣3)=﹣
m﹣3)=﹣![]() (m+2)2+3
(m+2)2+3
当m=﹣2时,DE有最大值为3
此时,S△ACD有最大值为![]() ×DE×4=2DE=6
×DE×4=2DE=6
∴四边形ABCD的面积的最大值为6+![]() =
=![]() .
.
(3)如图所示:
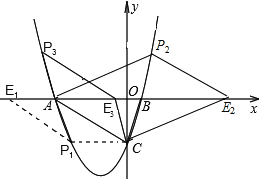
①过点C作CP1∥x轴交抛物线于点P1,过点P1作P1E1∥AC交x轴于点E1,此时四边形ACP1E1为平行四边形,
∵C(0,﹣3)
∴设P1(x,﹣3)
∴![]() x2+
x2+![]() x﹣3=﹣3
x﹣3=﹣3
解得x1=0,x2=﹣3
∴P1(﹣3,﹣3);
②平移直线AC交x轴于点E,交x轴上方的抛物线于点P,当AC=PE时,四边形ACEP为平行四边形,
∵C(0,﹣3)
∴设P(x,3),
∴![]() x2+
x2+![]() x﹣3=3,
x﹣3=3,
解得x=![]() 或x=
或x=![]() ,
,
∴P2(![]() ,3)或P3(
,3)或P3(![]() ,3)
,3)
综上所述存在3个点符合题意,坐标分别是P1(﹣3,﹣3)或P2(![]() ,3)或P3(
,3)或P3(![]() ,3).
,3).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
 在
在 的内部,点
的内部,点 关于
关于 、
、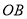 的对称点分别为
的对称点分别为 、
、 ,连接
,连接 交
交 、
、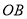 于点
于点 、
、 ,若
,若 ,则下列结论错误的是( )
,则下列结论错误的是( )
A.
 B.
B.
C.
 D.
D. 垂直平分
垂直平分
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC是等边三角形
(1) 如图1,点E在线段AB上,点D在射线CB上,且ED=EC,将△BCE绕点C顺时针旋转60°至△ACF,连接EF,猜想线段AB、DB、AF之间的数量关系
(2) 点E在线段BA的延长线上,其他条件与(1)中的一致,请在图2上将图形补充完整,并猜想证明线段AB、DB、AF之间的数量关系

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 中,
中, ,
, 于
于 ,
, 平分
平分 ,且
,且 于
于 ,与
,与 相交于点
相交于点 ,
, 是
是 边的中点,连接
边的中点,连接 与
与 相交于点
相交于点 ,下列结论正确的有( )个
,下列结论正确的有( )个①
 ;②
;② ;③
;③ ;④
;④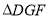 是等腰三角形;⑤
是等腰三角形;⑤ .
.
A.
 个B.
个B. 个C.
个C. 个D.
个D. 个
个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,
, 平分
平分 交边
交边 于点
于点 ,
, 分别是
分别是 ,
, 上的点,连结
上的点,连结 ,
, .若
.若 ,
, ,
, 则
则 的最小值是__________.
的最小值是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,点
,点 、
、 、
、 分别在
分别在 、
、 、
、 边上,且
边上,且 ,
, .
.
(1)求证:
 是等腰三角形;
是等腰三角形;(2)当
 时,求
时,求 的度数;
的度数;(3)当
 为多少度时,
为多少度时, ?请说明理由.
?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E是矩形ABCD边AD上的一个动点,且与点A、点D不重合,连结BE、CE,过点B作BF∥CE,过点C作CF∥BE,交点为F点,连接AF、DF分别交BC于点G、H,则下列结论错误的是( )
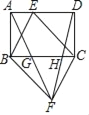
A. GH=
 BC B. S△BGF+S△CHF=
BC B. S△BGF+S△CHF= S△BCF
S△BCFC. S四边形BFCE=ABAD D. 当点E为AD中点时,四边形BECF为菱形
相关试题

