【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 、
、![]() 、
、![]() 分别在
分别在![]() 、
、![]() 、
、![]() 边上,且
边上,且![]() ,
,![]() .
.

(1)求证:![]() 是等腰三角形;
是等腰三角形;
(2)当![]() 时,求
时,求![]() 的度数;
的度数;
(3)当![]() 为多少度时,
为多少度时,![]() ?请说明理由.
?请说明理由.
参考答案:
【答案】(1)见解析(2)65°;(3)40°.
【解析】
(1)根据AB=AC可得∠B=∠C,即可求证△BDE≌△CEF,即可解题;
(2)根据全等三角形的性质得到∠CEF=∠BDE,于是得到∠DEF=∠B,根据等腰三角形的性质即可得到结论;
(3)由(2)得∠DEF=∠B,根据三角形的内角和与等腰三角形的性质即可求解.
(1)∵AB=AC,
∴∠B=∠C,
在△BDE和△CEF中,
∵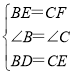 ,
,
∴△BDE≌△CEF(SAS),
∴DE=EF,
∴△DEF是等腰三角形;
(2)∵∠DEC=∠B+∠BDE,
即∠DEF+∠CEF=∠B+∠BDE,
∵△BDE≌△CEF,
∴∠CEF=∠BDE,
∴∠DEF=∠B,
又∵在△ABC中,AB=AC,∠A=50°,
∴∠B=65°,
∴∠DEF=65°;
(3)由(2)得∠DEF=∠B,
∵![]()
∴∠DEF=∠B=70°,
∴∠A=180°-2∠B=40°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 中,
中, ,
, 于
于 ,
, 平分
平分 ,且
,且 于
于 ,与
,与 相交于点
相交于点 ,
, 是
是 边的中点,连接
边的中点,连接 与
与 相交于点
相交于点 ,下列结论正确的有( )个
,下列结论正确的有( )个①
 ;②
;② ;③
;③ ;④
;④ 是等腰三角形;⑤
是等腰三角形;⑤ .
.
A.
 个B.
个B. 个C.
个C. 个D.
个D. 个
个 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A、B两点,点A在点B左侧,点B的坐标为(1,0),C(0,-3)
(1) 求抛物线的解析式;
(2) 若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值.
(3) 若点E在x轴上,点P在抛物线上,是否存在以A、C、E、P为顶点且以AC为一边的平行四边形?若存在,求点P的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,
, 平分
平分 交边
交边 于点
于点 ,
, 分别是
分别是 ,
, 上的点,连结
上的点,连结 ,
, .若
.若 ,
, ,
, 则
则 的最小值是__________.
的最小值是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E是矩形ABCD边AD上的一个动点,且与点A、点D不重合,连结BE、CE,过点B作BF∥CE,过点C作CF∥BE,交点为F点,连接AF、DF分别交BC于点G、H,则下列结论错误的是( )
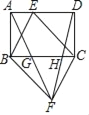
A. GH=
 BC B. S△BGF+S△CHF=
BC B. S△BGF+S△CHF= S△BCF
S△BCFC. S四边形BFCE=ABAD D. 当点E为AD中点时,四边形BECF为菱形
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列等式:①1=12;②2+3+4=32;③3+4+5+6+7=52;④4+5+6+7+8+9+10=72;…请根据上述规律判断下列等式正确的是( )
A. 1008+1009+…+3025=20162 B. 1009+1010+…+3026=20172
C. 1009+1010+…+3025=20172 D. 1010+1011+…+3029=20192
-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读下面的内容,再解决问题.
例题:若
 ,求
,求 和
和 的值.
的值.解:∵

∴

即

∴
 ,
,
∴
 ,
,
问题:(1)若
 ,求
,求 的值;
的值;(2)已知
 是
是 的三边长,满足
的三边长,满足 ,且
,且 中最长的边的长度为
中最长的边的长度为 ,求
,求 的取值范围.
的取值范围.
相关试题

