【题目】四边形ABCD为菱形,BD为对角线，在对角线BD上任取一点E，连接CE，把线段CE绕点C顺时针旋转得到线段CF，使得∠ECF=∠BCD ,点E的对应点为点F，连接DF.

(1)如图1，求证:BE=DF;

(2)如图2，若DF=CF=10, ∠DFC=2∠BDC,求菱形ABCD的边长.

参考答案：

【答案】（10证明见解析；（2） .

【解析】试题分析:(1)先根据∠ECF=∠BCD,可求证∠ECB=∠DCF,由旋转可得:EC=FC,由菱形的性质可得:BC=CD,根据SAS可证△BCE≌△DCF,所以BE=DF,(2)根据DF=CF=10,可得DF=10,CF=4,由 ∠DFC=2∠BDC,可得: ∠BEF=2∠BDC,根据三角形的性质性质可得:

∠BEF=∠BDC+∠ECD,所以∠BDC=∠ECD,所以BE=CE=CF=4,所以BD=14,利用相似三角形的判定可证△BCD∽△CED,根据相似三角形的性质可得: ,然后计算可得DC.

试题解析:(1)因为∠ECF=∠BCD,

所以∠ECF－∠ECD=∠BCD－∠ECD,

所以∠ECB=∠DCF,

由旋转可得: EC=FC,

因为菱形ABCD,

所以BC=CD,

在△BCE和△DCF中,

,

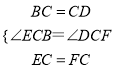所以△BCE≌△DCF,

所以BE=DF,

(2)因为DF=CF=10,所以DF=10,CF=4,

因为∠DFC=2∠BDC,所以 ∠BEF=2∠BDC,

又因为∠BEF=∠BDC+∠ECD,

所以∠BDC=∠ECD,

所以BE=CE=CF=4,所以BD=14,

因为△BCD和△CED是等腰三角形,且∠BDC是公共角

所以△BCD∽△CED,所以,即,解得CD=,

所以菱形的边长为.

关闭