【题目】如图,AB是⊙O的弦,点C在⊙O外,OC⊥OA,并交AB于点P,且CP=CB. 
(1)判断CB与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为3,OP=1,求弦AB的长.
参考答案:
【答案】
(1)解:∵OA=OB
∴∠OAB=∠OBA
∵CP=CB
∴∠CPB=∠CBP
在Rt△AOP中
∠A+∠APO=90°
∴∠OBA+∠CBP=90° 即:∠OBC=90°
∴OB⊥CB
又∵OB是半径
∴CB与⊙O相切
(2)解:设BC=CP=x
在Rt△OBC中
OC2=BC2+OB2
即:(x+1)2=x2+32
解之得:x=4,即:CP=4
在Rt△OBC中
AP= ![]() =
= ![]() =
= ![]()
作CH⊥AB于H
∵∠AOP=∠CHP=90°,∠APO=∠CPH
∴△OAP∽△HCP
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴HP= ![]()
∵CB=CP,CH⊥PB
∴PB=2PH= ![]()
![]()
∴AB=AP+PB= ![]()
![]() .
.
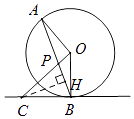
【解析】(1)根据等边对等角得∠CPB=∠CBP,根据垂直的定义得∠OBC=90°,即OB⊥CB,则CB与⊙O相切;(2)设BC=CP=x,在Rt△OBC中,根据勾股定理得出CP=4,再在Rt△OBC中,由勾股定理得出AP,作CH⊥AB,可证明△OAP∽△HCP,得出HP,由垂径定理得出PB=2PH,即可得出AB=AP+PB的长.
【考点精析】根据题目的已知条件,利用勾股定理的概念和垂径定理的相关知识可以得到问题的答案,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
-
科目: 来源: 题型:
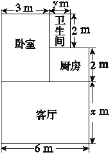
查看答案和解析>>【题目】丁丁家买了一套安置房,地面结构如图所示.
(1)写出用含x、y的式子表示地面的总面积;
(2)如果x=4 m,y=1.5 m,铺1 m2地砖的平均费用为80元,求铺地砖的总费用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有这样一道题:计算(2x3-3x2y-2xy2)-(x3-2xy2+y3)+(-x3+3x2y-y3)的值,其中x=-
 ,y=-2.甲同学把“x=-
,y=-2.甲同学把“x=- ”错抄成“x=
”错抄成“x= ”.但他计算的结果是正确的,请你分析这是什么原因.
”.但他计算的结果是正确的,请你分析这是什么原因. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,顺次连接矩形ABCD四边的中点得到四边形A1B1C1D1,然后顺次连接四边形A1B1C1D1的中点得到四边形A2B2C2D2,再顺次连接四边形A2B2C2D2四边的中点得到四边形A3B3C3D3,…,已知AB=6, BC=8,按此方法得到的四边形A5B5C5D5的周长为(______).

-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC纸片中,∠ACB=90°,AC=6,BC=8,P是AB边上一点,连接CP.沿CP把Rt△ABC纸片裁开,要使△ACP是等腰三角形,那么AP的长度是________
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A=3a2b﹣2ab2+abc,小明同学错将“2A﹣B“看成”2A+B“,算得结果为4a2b﹣3ab2+4abc.
(1)计算B的表达式;
(2)求出2A﹣B的结果;
(3)小强同学说(2)中的结果的大小与c的取值无关,对吗?若a=
 ,b=
,b= ,
,求(2)中式子的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AD=5,AB=8,点E为射线DC上的一个动点,把△ADE沿AE折叠点.D的对应点为D′.
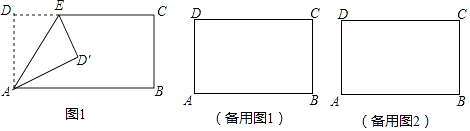
(1)求点D′刚好落在对角线AC上时,D′C的长;
(2)求点D′刚好落在此对称轴上时,线段DE的长.
相关试题

