【题目】如图,顺次连接矩形ABCD四边的中点得到四边形A1B1C1D1,然后顺次连接四边形A1B1C1D1的中点得到四边形A2B2C2D2,再顺次连接四边形A2B2C2D2四边的中点得到四边形A3B3C3D3,…,已知AB=6, BC=8,按此方法得到的四边形A5B5C5D5的周长为(______).

参考答案:
【答案】5
【解析】根据菱形和矩形的性质以及三角形中位线的性质以及勾股定理求出四边形各边长得出规律求出即可.
解:∵矩形ABCD中,AB=6,AD=8,顺次连结矩形形ABCD各边中点,
∴四边形A1B1C1D1是菱形,
∴A1B1=5,
∴四边形A1B1C1D1的周长是:5×4=20,
同理可得出:A2D2=8×![]() =4,C2D2=
=4,C2D2=![]() AB=
AB=![]() ×6=3,
×6=3,
∴A3D3=![]() ,
,
∴四边形A3B3C3D3的周长是:![]() ×4=10,
×4=10,
…
∴四边形A5B5C5D5周长是:![]() ×
×![]() ×4=5.
×4=5.
故答案为:5.
“点睛”此题主要考查了菱形的性质以及矩形的性质和中点四边形的性质等知识,根据已知得出边长变化规律是解题关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知ABCD中,AD=2AB,F是BC的中点,作AE⊥CD,垂足E在线段CD上,连结EF、AF,下列结论:①2∠BAF=∠BAD;②EF=AF;③S△ABF≤S△AEF;④∠BFE=3∠CEF.中一定成立的是( )

A. ①②④ B. ①③ C. ②③④ D. ①②③④
-
科目: 来源: 题型:
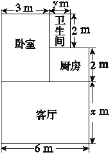
查看答案和解析>>【题目】丁丁家买了一套安置房,地面结构如图所示.
(1)写出用含x、y的式子表示地面的总面积;
(2)如果x=4 m,y=1.5 m,铺1 m2地砖的平均费用为80元,求铺地砖的总费用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有这样一道题:计算(2x3-3x2y-2xy2)-(x3-2xy2+y3)+(-x3+3x2y-y3)的值,其中x=-
 ,y=-2.甲同学把“x=-
,y=-2.甲同学把“x=- ”错抄成“x=
”错抄成“x= ”.但他计算的结果是正确的,请你分析这是什么原因.
”.但他计算的结果是正确的,请你分析这是什么原因. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的弦,点C在⊙O外,OC⊥OA,并交AB于点P,且CP=CB.

(1)判断CB与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为3,OP=1,求弦AB的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC纸片中,∠ACB=90°,AC=6,BC=8,P是AB边上一点,连接CP.沿CP把Rt△ABC纸片裁开,要使△ACP是等腰三角形,那么AP的长度是________
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A=3a2b﹣2ab2+abc,小明同学错将“2A﹣B“看成”2A+B“,算得结果为4a2b﹣3ab2+4abc.
(1)计算B的表达式;
(2)求出2A﹣B的结果;
(3)小强同学说(2)中的结果的大小与c的取值无关,对吗?若a=
 ,b=
,b= ,
,求(2)中式子的值.
相关试题

