【题目】如图,矩形ABCD中,AD=5,AB=8,点E为射线DC上的一个动点,把△ADE沿AE折叠点.D的对应点为D′. 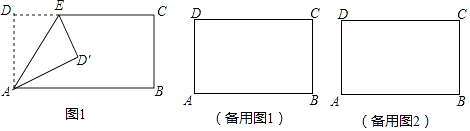
(1)求点D′刚好落在对角线AC上时,D′C的长;
(2)求点D′刚好落在此对称轴上时,线段DE的长.
参考答案:
【答案】
(1)解:如图1,在Rt△ABC中,
∵∴AD′=AD=5,
∵AC= ![]() =
= ![]() =
= ![]() ,
,
∴CD′=AC﹣AD′= ![]() ﹣5
﹣5
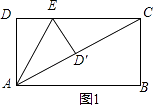
(2)解:①当D′落在对称轴GH上,
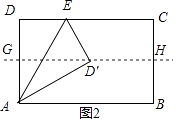
∵GH是矩形对称轴,
∴AC= ![]() AD,
AD,
由翻折的性质得:AD′=AD,∠DAE= ![]() ∠DAD′,
∠DAD′,
∴GA= ![]() AD′,
AD′,
∴在Rt△AGD′中,∠GAD′=60°,
∴∠DAE= ![]() ∠DAD′=30°,
∠DAD′=30°,
在Rt△ADE中,
∵tan∠DAE= ![]() ,即:tan30°=
,即:tan30°= ![]() ,
,
∴DE= ![]() ,
,
②当D′落在对称轴MN上,又分两种情况,
第一种:点E在DC上,如图3,
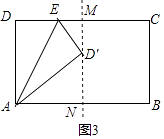
∵MN是矩形对称轴,
∴DM=AN=4,
由翻折得:AD′=AD,
在Rt△AND′中,
D′N= ![]() =3,
=3,
∴D′M=MN﹣D′N=5﹣3=2,
设DE=ED′=x,
在Rt△EAD′中,
ED′2=EM2+MD′2,
即:x2=(4﹣x)2+22,
解之得:x= ![]() ,即DE=
,即DE= ![]() ,
,
第二种:点E在DC延长线上,如图4,方法同上,DE=10.

综上所述,点D′落在矩形对称轴上时,DE的长为 ![]() 或
或 ![]() 或10.
或10.
【解析】(1)如图1,在Rt△ABC中,根据勾股定理即可得到结论;(2)①当D′落在对称轴GH上,由翻折的性质得到AD′=AD,∠DAE= ![]() ∠DAD′,求得GA=
∠DAD′,求得GA= ![]() AD′,根据三角形的内角和得到∠DAE=
AD′,根据三角形的内角和得到∠DAE= ![]() ∠DAD′=30°,根据三角函数的定即可得到结论;②当D′落在对称轴MN上,又分两种情况,第一种:点E在DC上,如图3,得到DM=AN=4,由翻折的性质得到AD′=AD,在Rt△AND′中,由勾股定理得到D′N=
∠DAD′=30°,根据三角函数的定即可得到结论;②当D′落在对称轴MN上,又分两种情况,第一种:点E在DC上,如图3,得到DM=AN=4,由翻折的性质得到AD′=AD,在Rt△AND′中,由勾股定理得到D′N= ![]() =3,得到D′M=MN﹣D′N=5﹣3=2,设DE=ED′=x,在Rt△EAD′中,根据勾股定理得到DE=
=3,得到D′M=MN﹣D′N=5﹣3=2,设DE=ED′=x,在Rt△EAD′中,根据勾股定理得到DE= ![]() ,第二种:点E在DC延长线上,同理得到结论.
,第二种:点E在DC延长线上,同理得到结论.
【考点精析】本题主要考查了矩形的性质和翻折变换(折叠问题)的相关知识点,需要掌握矩形的四个角都是直角,矩形的对角线相等;折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的弦,点C在⊙O外,OC⊥OA,并交AB于点P,且CP=CB.

(1)判断CB与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为3,OP=1,求弦AB的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC纸片中,∠ACB=90°,AC=6,BC=8,P是AB边上一点,连接CP.沿CP把Rt△ABC纸片裁开,要使△ACP是等腰三角形,那么AP的长度是________
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A=3a2b﹣2ab2+abc,小明同学错将“2A﹣B“看成”2A+B“,算得结果为4a2b﹣3ab2+4abc.
(1)计算B的表达式;
(2)求出2A﹣B的结果;
(3)小强同学说(2)中的结果的大小与c的取值无关,对吗?若a=
 ,b=
,b= ,
,求(2)中式子的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明有5张写着不同的数字的卡片,请你按要求抽出卡片,完成下列各问题:

(1)从中取出2张卡片,使这2张卡片上数字乘积最大,最大值是 ;
(2)从中取出2张卡片,使这2张卡片上数字相除的商最小,最小值是 ;
(3)从中取出4张卡片,用学过的运算方法,使结果为24.写出运算式子:
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两台智能机器人从同一地点P出发,沿着笔直的路线行走了450cm到点Q.甲比乙先出发,乙出发一段时间后速度提高为原来的2倍.甲匀速走完全程.两机器人行走的路程y(cm)与时间x(s)之间的函数图象如图所示.根据图象所提供的信息解答下列问题:
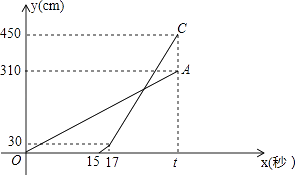
(1)乙比甲晚出发秒,乙提速前的速度是每秒cm,t=;
(2)当x为何值时,乙追上了甲?
(3)若两台机器人到达终点Q后迅速折返,并保持折返前的速度继续匀速行走返回到点P,乙比甲早到多长时间? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,AO⊥BC,DO⊥OE.
(1)不添加其他条件情况下,请尽可能多地写出图中有关角的等量关系(至少3个);
(2)如果∠COE
 350,求∠BOD的度数.
350,求∠BOD的度数.
相关试题

