【题目】如图,在平面直角坐标系中,O为坐标原点,在长方形OABC中,点A(10,0),C(0,4),D为OA的中点,P为BC边上一点.若△POD为等腰三角形,求所有满足条件的点P的坐标.
参考答案:
【答案】点P的坐标为(2.5,4)或(3,4)或(2,4)或(8,4).
【解析】试题分析:由矩形的性质得出∠OCB=90°,OC=4,BC=OA=10,求出OD=AD=5,分情况讨论:①当PO=PD时;②当OP=OD时;③当DP=DO时;根据线段垂直平分线的性质或勾股定理即可求出点P的坐标.
试题解析:解:∵四边形OABC是长方形,
∴∠OCB=90°,OC=4,BC=OA=10.
∵D为OA的中点,
∴OD=AD=5.
①当PO=PD时,点P在OD的垂直平分线上,
∴点P的坐标为(2.5,4).
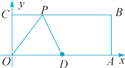
②当OP=OD时,如解图①所示.
则OP=OD=5,PC=![]() =3,
=3,
∴点P的坐标为(3,4).
①
③当DP=DO时,过点P作PE⊥OA于点E,
则∠PED=90°,DE=![]() =3.
=3.
分两种情况讨论:当点E在点D的左侧时,如解图②所示.
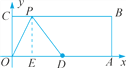
②
此时OE=5-3=2,
∴点P的坐标为(2,4).
当点E在点D的右侧时,如解图③所示.
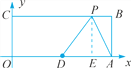
③
此时OE=5+3=8,
∴点P的坐标为(8,4).
综上所述,点P的坐标为(2.5,4)或(3,4)或(2,4)或(8,4).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线a∥b,∠3=131°,求∠1、∠2的度数(填理由或数学式)
解:∵∠3=131° ( )
又∵∠3=∠1 ()
∴∠1= ( )
∵a∥b ( )
∴∠1+∠2=180° ( )
∴∠2= ( ).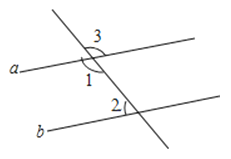
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2﹣2x+m﹣1=0有两个实数根x1,x2.
(1)求m的取值范围;
(2)当x12+x22=6x1x2时,求m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】单项式﹣3πxy2z3的系数和次数分别是( )
A.﹣π,5
B.﹣1,6
C.﹣3π,6
D.﹣3,7 -
科目: 来源: 题型:
查看答案和解析>>【题目】清朝康熙皇帝是我国历史上对数学很有兴趣的帝王近日,西安发现了他的数学专著,其中有一文《积求勾股法》,它对“三边长为3、4、5的整数倍的直角三角形,已知面积求边长”这一问题提出了解法:“若所设者为积数(面积),以积率六除之,平方开之得数,再以勾股弦各率乘之,即得勾股弦之数”.用现在的数学语言表述是:“若直角三角形的三边长分别为3、4、5的整数倍,设其面积为S,则第一步:
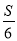 =m;第二步:
=m;第二步: 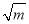 =k;第三步:分别用3、4、5乘以k,得三边长”.
=k;第三步:分别用3、4、5乘以k,得三边长”.(1)当面积S等于150时,请用康熙的“积求勾股法”求出这个直角三角形的三边长;
(2)你能证明“积求勾股法”的正确性吗?请写出证明过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】冬季某天我国三个城市的最高气温分别是﹣10℃,1℃,﹣7℃,它们任意两城市中最大的温差是( )
A.11℃
B.17℃
C.8℃
D.3℃ -
科目: 来源: 题型:
查看答案和解析>>【题目】求下列各式中x的值.
(1)x2=5
(2)x2﹣5=
(3)(x﹣2)2=125
(4)(y+3)3+64=0.
相关试题

