【题目】已知关于x的一元二次方程x2﹣2x+m﹣1=0有两个实数根x1,x2.
(1)求m的取值范围;
(2)当x12+x22=6x1x2时,求m的值.
参考答案:
【答案】(1)m≤2;(2)![]()
【解析】
试题分析:(1)根据一元二次方程x2﹣2x+m﹣1=0有两个实数根,可得△≥0,据此求出m的取值范围;
(2)根据根与系数的关系求出x1+x2,x1x2的值,代入x12+x22=6x1x2求解即可.
试题解析:(1)∵原方程有两个实数根,
∴△=(﹣2)2﹣4(m﹣1)≥0,
整理得:4﹣4m+4≥0,
解得:m≤2;
(2)∵x1+x2=2,x1x2=m﹣1,x12+x22=6x1x2,
∴(x1+x2)2﹣2x1x2=6x1x2,
即4=8(m﹣1),
解得:m=![]() .
.
∵m=![]() <2,
<2,
∴符合条件的m的值为![]() .
.
-
科目: 来源: 题型:
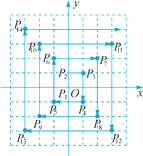
查看答案和解析>>【题目】如图,在平面直角坐标系中,每个最小方格的边长均为1个单位,P1,P2,P3,…均在格点上,其顺序按图中“→”方向排列,如:点P1(0,0),P2(0,1),P3(1,1),P4(1,-1),P5(-1,-1),P6(-1,2),….根据这个规律,求点P2018的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数据-3,-2,0,6,6,13,20,35则它的中位数和众数各是( )
A. 6和6 B. 3和6 C. 6和3 D. 9.5和6
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线a∥b,∠3=131°,求∠1、∠2的度数(填理由或数学式)
解:∵∠3=131° ( )
又∵∠3=∠1 ()
∴∠1= ( )
∵a∥b ( )
∴∠1+∠2=180° ( )
∴∠2= ( ).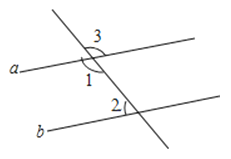
-
科目: 来源: 题型:
查看答案和解析>>【题目】单项式﹣3πxy2z3的系数和次数分别是( )
A.﹣π,5
B.﹣1,6
C.﹣3π,6
D.﹣3,7 -
科目: 来源: 题型:
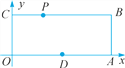
查看答案和解析>>【题目】如图,在平面直角坐标系中,O为坐标原点,在长方形OABC中,点A(10,0),C(0,4),D为OA的中点,P为BC边上一点.若△POD为等腰三角形,求所有满足条件的点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】清朝康熙皇帝是我国历史上对数学很有兴趣的帝王近日,西安发现了他的数学专著,其中有一文《积求勾股法》,它对“三边长为3、4、5的整数倍的直角三角形,已知面积求边长”这一问题提出了解法:“若所设者为积数(面积),以积率六除之,平方开之得数,再以勾股弦各率乘之,即得勾股弦之数”.用现在的数学语言表述是:“若直角三角形的三边长分别为3、4、5的整数倍,设其面积为S,则第一步:
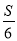 =m;第二步:
=m;第二步: 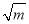 =k;第三步:分别用3、4、5乘以k,得三边长”.
=k;第三步:分别用3、4、5乘以k,得三边长”.(1)当面积S等于150时,请用康熙的“积求勾股法”求出这个直角三角形的三边长;
(2)你能证明“积求勾股法”的正确性吗?请写出证明过程.
相关试题

