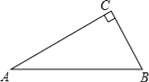
【题目】如图,△ABC中,∠C=90°,∠A=30°.
(1)用尺规作图作AB边上的垂直平分线DE,交AC于点D,交AB于点E.(保留作图痕迹,不要求写作法和证明)
(2)连接BD,求证:DE=CD.
参考答案:
【答案】(1)作图见解析(2)证明见解析
【解析】试题分析:(1)利用基本作图(作已知线段的垂直平分线)作DE垂直平分AB;
(2)先利用线段垂直平分线的性质得到DA=DB,则∠DBA=∠A=30°,再证明BD平分∠ABC,然后根据角平分线的性质定理可得到结论.
试题解析:(1)如图,DE为所作;
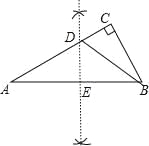
(2)如图,
∵DE垂直平分AB,
∴DA=DB,
∴∠DBA=∠A=30°,
∵∠ABC=90°﹣∠A=60°,
∴∠CBD=30°,
即BD平分∠ABC,
而DE⊥AB,DC⊥BC,
∴DE=DC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】a,b,c是同一平面内的三条不同直线,下列命题是假命题的是( )
A. 若a∥b,b∥c,则a∥cB. 若a⊥b,b⊥c,则a⊥c
C. 若a∥b, b⊥c,则a⊥cD. 若a⊥b,b⊥c,则a∥c
-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,∠ACB=90°,AC=BC,D为BC中点,CE⊥AD于E,BF∥AC交CE的延长线于F.
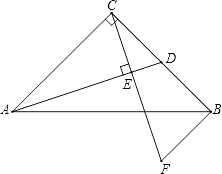
(1)求证:△ACD≌△CBF;
(2)求证:AB垂直平分DF. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,“赵爽弦图”由4个全等的直角三角形拼成,在Rt△ABC中,∠ACB=90°,AC=b,BC=a,请你利用这个图形解决下列问题:

(1)证明勾股定理;
(2)说明a2+b2≥2ab及其等号成立的条件. -
科目: 来源: 题型:
查看答案和解析>>【题目】点P在第一象限,且点P到x轴距离为5,到y轴距离为3,则点P的坐标为___.
-
科目: 来源: 题型:
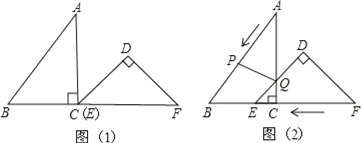
查看答案和解析>>【题目】把Rt△ABC和Rt△DEF按如图(1)摆放(点C与E重合),点B、C(E)、F在同一条直线上.已知:∠ACB=∠EDF=90°,∠DEF=45°,AC=8cm,BC=6cm,EF=10cm.如图(2),△DEF从图(1)的位置出发,以1cm/s的速度沿CB向△ABC匀速移动,在△DEF移动的同时,点P从△ABC的顶点A出发,以2cm/s的速度沿AB向点B匀速移动;当点P移动到点B时,点P停止移动,△DEF也随之停止移动.DE与AC交于点Q,连接PQ,设移动时间为t(s).
(1)用含t的代数式表示线段AP和AQ的长,并写出t的取值范围;
(2)连接PE,设四边形APEQ的面积为y(cm2),试探究y的最大值;
(3)当t为何值时,△APQ是等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P位于x轴下方,距离x轴5个单位,位于y轴右方,距离y轴3个单位,那么P点的坐标是( )
A.(5,-3) B.(3,-5) C.(-5,3) D.(-3,5)
相关试题

