【题目】在Rt△ABC中,∠ACB=90°,AC=BC,D为BC中点,CE⊥AD于E,BF∥AC交CE的延长线于F.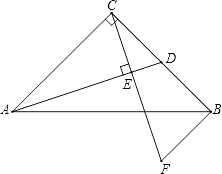
(1)求证:△ACD≌△CBF;
(2)求证:AB垂直平分DF.
参考答案:
【答案】
(1)解:∵在Rt△ABC中,∠ACB=90°,AC=BC,
∴∠CAB=∠CBA=45°,
∵CE⊥AD,
∴∠CAD=∠BCF,
∵BF∥AC,
∴∠FBA=∠CAB=45°
∴∠ACB=∠CBF=90°,
在△ACD与△CBF中,
∵ 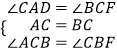 ,
,
∴△ACD≌△CBF;
(2)解:证明:∵∠BCE+∠ACE=90°,∠ACE+∠CAE=90°,
∴∠BCE=∠CAE.
∵AC⊥BC,BF∥AC.
∴BF⊥BC.
∴∠ACD=∠CBF=90°,
在△ACD与△CBF中,
∵ 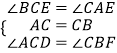 ,
,
∴△ACD≌△CBF,
∴CD=BF.
∵CD=BD= ![]() BC,
BC,
∴BF=BD.
∴△BFD为等腰直角三角形.
∵∠ACB=90°,CA=CB,
∴∠ABC=45°.
∵∠FBD=90°,
∴∠ABF=45°.
∴∠ABC=∠ABF,即BA是∠FBD的平分线.
∴BA是FD边上的高线,BA又是边FD的中线,
即AB垂直平分DF
【解析】(1)根据∠ACB=90°,AC=BC,求得∠CAD=∠BCF,再利用BF∥AC,求得∠ACB=∠CBF=90°,然后利用ASA即可证明△ACD≌△CBF,
(2)利用同角的余角相等得出,∠BCE=∠CAE,再根据平行线的性质得出∠ACD=∠CBF=90°,然后由ASA判定△ACD≌△CBF得到BF=BD,再根据角度之间的数量关系求出∠ABC=∠ABF,即BA是∠FBD的平分线,从而利用等腰三角形三线合一的性质求证即可
【考点精析】根据题目的已知条件,利用平行线的性质和等腰三角形的性质的相关知识可以得到问题的答案,需要掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;等腰三角形的两个底角相等(简称:等边对等角).
-
科目: 来源: 题型:
查看答案和解析>>【题目】为促进我市经济的快速发展,加快道路建设,某高速公路建设工程中需修隧道AB,如图,在山外一点C测得BC距离为200m,∠CAB=54°,∠CBA=30°,求隧道AB的长.(参考数据:sin54°≈0.81,cos54°≈0.59,tan54°≈1.38,
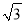 ≈1.73,精确到个位)
≈1.73,精确到个位)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形网格中的每个小正方形边长都是1.
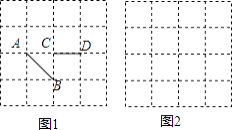
(1)图1中已知线段AB、CD,画线段EF,使它与AB、CD组成轴对称图形(要求:画出一个即可);
(2)在图2中画出一个以格点为端点长为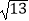 的线段.
的线段. -
科目: 来源: 题型:
查看答案和解析>>【题目】a,b,c是同一平面内的三条不同直线,下列命题是假命题的是( )
A. 若a∥b,b∥c,则a∥cB. 若a⊥b,b⊥c,则a⊥c
C. 若a∥b, b⊥c,则a⊥cD. 若a⊥b,b⊥c,则a∥c
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,“赵爽弦图”由4个全等的直角三角形拼成,在Rt△ABC中,∠ACB=90°,AC=b,BC=a,请你利用这个图形解决下列问题:

(1)证明勾股定理;
(2)说明a2+b2≥2ab及其等号成立的条件. -
科目: 来源: 题型:
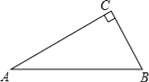
查看答案和解析>>【题目】如图,△ABC中,∠C=90°,∠A=30°.
(1)用尺规作图作AB边上的垂直平分线DE,交AC于点D,交AB于点E.(保留作图痕迹,不要求写作法和证明)
(2)连接BD,求证:DE=CD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P在第一象限,且点P到x轴距离为5,到y轴距离为3,则点P的坐标为___.
相关试题

