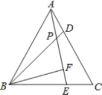
【题目】如图,△ABC为等边三角形,D、E分别是AC、BC上的点,且AD=CE,AE与BD相交于点P,BF⊥AE于点F.若BP=4,则PF的长( )
A. 2 B. 3 C. 1 D. 8
参考答案:
【答案】A
【解析】
试题证△ABD≌△CAE,推出∠ABD=∠CAE,求出∠BPF=∠APD=60°,得出∠PBF=30°,根据含30度角的直角三角形性质求出即可.
解:∵△ABC是等边三角形,
∴AB=AC.
∴∠BAC=∠C.
在△ABD和△CAE中,
 ,
,
∴△ABD≌△CAE(SAS).
∴∠ABD=∠CAE.
∴∠APD=∠ABP+∠PAB=∠BAC=60°.
∴∠BPF=∠APD=60°.
∵∠BFP=90°,∠BPF=60°,
∴∠PBF=30°.
∴PF=![]() .
.
故选;A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】求代数式的值.
(1)(6a2﹣2ab)﹣2(3a2+4ab﹣
 b2)其中a=
b2)其中a=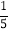 ,b=﹣1.
,b=﹣1.(2)已知A=a2﹣2ab+b2,B=a2+2ab+b2
①求2A﹣B;
②如果2A﹣3B+C=0,那么C的表达式是什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D.
(1)当∠BQD=30°时,求AP的长;
(2)证明:在运动过程中,点D是线段PQ的中点;
(3)当运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果变化请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】“十一”黄金周期间,深圳世界之窗风景区在7天假期中每天旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数):
日期
1日
2日
3日
4日
5日
6日
7日
人数变化
单位:万人
+1.6
+0.8
+0.4
﹣0.4
﹣0.8
+0.2
﹣1.2
(1)请判断七天内游客人数最多的是 日,最少的是 日.
(2)以9月30日的游客人数为0点,用折线统计图表示这7天的游客人数的变化情况.
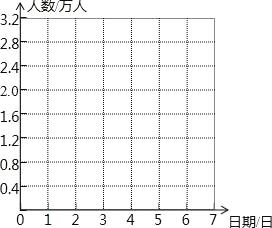
-
科目: 来源: 题型:
查看答案和解析>>【题目】某数学兴趣小组在本校九年级学生中以“你最喜欢的一项体育运动”为主题进行了抽样调查,并将调查结果绘制成如图图表:
项目
篮球
乒乓球
羽毛球
跳绳
其他
人数
a
12
10
5
8
请根据图表中的信息完成下列各题:
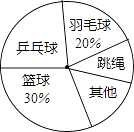
(1)本次共调查学生名;
(2)a= , 表格中五个数据的中位数是;
(3)在扇形图中,“跳绳”对应的扇形圆心角是;
(4)如果该年级有450名学生,那么据此估计大约有人最喜欢“乒乓球”. -
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列等式:
第一个等式:a1=
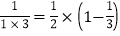
第二个等式:a2=
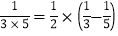
第三个等式:a3=
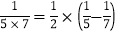
……
按以上规律解答下列问题:
(1)列出第五个等式:a5=
(2)计算a1+a2+a3+a4+a5的结果.
(3)计算a1+a2+a3+……+an﹣1+an的结果.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,BE交对角线AC于点E,DF∥BE交AC于点F.

(1)写出图中所有的全等三角形(不得添加辅助线);
(2)求证:BE=DF.
相关试题

