【题目】某数学兴趣小组在本校九年级学生中以“你最喜欢的一项体育运动”为主题进行了抽样调查,并将调查结果绘制成如图图表:
项目 | 篮球 | 乒乓球 | 羽毛球 | 跳绳 | 其他 |
人数 | a | 12 | 10 | 5 | 8 |
请根据图表中的信息完成下列各题: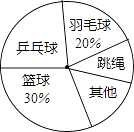
(1)本次共调查学生名;
(2)a= , 表格中五个数据的中位数是;
(3)在扇形图中,“跳绳”对应的扇形圆心角是;
(4)如果该年级有450名学生,那么据此估计大约有人最喜欢“乒乓球”.
参考答案:
【答案】
(1)50
(2)15;10
(3)36°
(4)108
【解析】解:(1)设本次共调查了x名学生, ∵由统计表中的数据可知喜欢羽毛球的有10人,由扇形统计图可知,喜欢羽毛球的人数是总人数的20%,
∴ ![]() ×100%=20%,解得x=50(人);
×100%=20%,解得x=50(人);
2)∵喜欢篮球的人数占调查人数的30%,共有50人参加调查,
∴a=50×30%=15(人);
∴这五个数据的中位数是:10;
3)∵由于喜欢跳绳的人数是5人,
∴ ![]() =
= ![]() ,
,
∴“跳绳”对应的扇形圆心角的度数= ![]() ×360°=36°;
×360°=36°;
4)∵喜欢乒乓球的人数是12人,
∴喜欢乒乓球的人数占参加调查人数的百分比为: ![]() ×100%=24%,
×100%=24%,
∵该年级有450名学生,
∴最喜欢“乒乓球”的人数大约有:450×24%=108(人).
【考点精析】本题主要考查了统计表和扇形统计图的相关知识点,需要掌握制作统计表的步骤:(1)收集整理数据.(2)确定统计表的格式和栏目数量,根据纸张大小制成表格.(3)填写栏目、各项目名称及数据.(4)计算总计和合计并填入表中,一般总计放在横栏最左格,合计放在竖栏最上格.(5)写好表格名称并标明制表时间;能清楚地表示出各部分在总体中所占的百分比.但是不能清楚地表示出每个项目的具体数目以及事物的变化情况才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D.
(1)当∠BQD=30°时,求AP的长;
(2)证明:在运动过程中,点D是线段PQ的中点;
(3)当运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果变化请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】“十一”黄金周期间,深圳世界之窗风景区在7天假期中每天旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数):
日期
1日
2日
3日
4日
5日
6日
7日
人数变化
单位:万人
+1.6
+0.8
+0.4
﹣0.4
﹣0.8
+0.2
﹣1.2
(1)请判断七天内游客人数最多的是 日,最少的是 日.
(2)以9月30日的游客人数为0点,用折线统计图表示这7天的游客人数的变化情况.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC为等边三角形,D、E分别是AC、BC上的点,且AD=CE,AE与BD相交于点P,BF⊥AE于点F.若BP=4,则PF的长( )
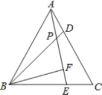
A. 2 B. 3 C. 1 D. 8
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列等式:
第一个等式:a1=
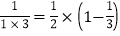
第二个等式:a2=
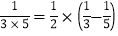
第三个等式:a3=
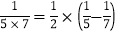
……
按以上规律解答下列问题:
(1)列出第五个等式:a5=
(2)计算a1+a2+a3+a4+a5的结果.
(3)计算a1+a2+a3+……+an﹣1+an的结果.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,BE交对角线AC于点E,DF∥BE交AC于点F.

(1)写出图中所有的全等三角形(不得添加辅助线);
(2)求证:BE=DF. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,点C是⊙O上一点,∠BAC的平分线AD交⊙O于点D,过点D垂直于AC的直线交AC的延长线于点E.

(1)求证:DE是⊙O的切线;
(2)如图AD=5,AE=4,求⊙O的直径.
相关试题

