【题目】如图,抛物线y1=﹣ax2+2ax﹣a﹣3(a>0)和y2=a(x+1)2﹣1(a>0)的顶点分别为M、N,与y轴分别交于E、F.
(1)①函数y1=﹣ax2+2ax﹣a﹣3(a>0)的最大值是;
②当y1、y2的值都随x的增大而增大时,自变量x的取值范围是;
(2)当EF=MN时,求a值,并判断四边形EMFN是何种特殊的四边形;
(3)若y2=a(x+1)2﹣1(a>0)的图象与x轴的右交点为A(m,0),当△AMN为等腰三角形时,求方程a(x+1)2﹣1=0的解.
参考答案:
【答案】
(1)-3;﹣1≤x≤1
(2)
解:∵y1=﹣a(x﹣1)2﹣3,y2=a(x+1)2﹣1,
∴N(﹣1,﹣1),M(1,﹣3).
由两点间的距离公式可知:MN=2 ![]() .
.
令x=0得:y1=﹣a﹣3,y2=a﹣1.
∴F(0,a﹣1),E(0,﹣a﹣3).
∴EF=2a+2.
∵EF=MN,
∴2a+2=2 ![]() ,解得:a=
,解得:a= ![]() ﹣1.
﹣1.

作NC⊥y轴于C,MD⊥y轴于D
∴NC=1,FC=a,MD=1,DE=a
∵在Rt△CNF和Rt△MDE中,  ,
,
∴△NCF≌MDE.
∴NF=EM,∠NFC=∠DEM
∴NF‖EM
∴四边形EMFN是平行四边形
又∵NM=EF
∴四边形EMFN是矩形
(3)
解:∵A(m,0)M(1,﹣3)N(﹣1,﹣1),
∴AN2=m2+2m+2,AM2=m2﹣2m+10,MN2=8.
①若AN=AM,则m2+2m+2=m2﹣2m+10,解得:m=2,
∴方程a(x+1)2﹣1=0的一个解为x=2,
根据抛物线对称性,可知方程的另一个解为x=﹣4.
②若AN=MN,则m2+2m+2=8,解得:m=﹣1+ ![]() 或m=﹣1﹣
或m=﹣1﹣ ![]() (舍去),
(舍去),
所以方程a(x+1)2﹣1=0的一个解为x=﹣1+ ![]() ,
,
根据抛物线对称性,可知方程的另一个解为x=﹣1﹣ ![]() .
.
③若AM=MN,所以m2﹣2m+10=8,
此方程无解,所以此种情况不成立
综上所述当△AMN为等腰三角形时,方程a(x+1)2﹣1=0的解为x1=2,x2=﹣4或x1=﹣1 ![]() 或x2=﹣1﹣
或x2=﹣1﹣ ![]()
【解析】解:(1)①y1=﹣ax2+2ax﹣a﹣3=﹣a(x2﹣2x+1)﹣3=﹣a(x﹣1)2﹣3,
∴函数y1=﹣ax2+2ax﹣a﹣3(a>0)的最大值是﹣3.
所以答案是:﹣3.
②∵y1=﹣a(x﹣1)2﹣3,﹣a<0,
∴当x≤1时,y随x的增大而增大.
∵y2=a(x+1)2﹣1(a>0),
∴当x≥﹣1时,y随x的增大而增大.
∴当﹣1≤x≤1时,y1、y2的值都随x的增大而增大.
【考点精析】利用二次函数的概念和二次函数的最值对题目进行判断即可得到答案,需要熟知一般地,自变量x和因变量y之间存在如下关系:一般式:y=ax2+bx+c(a≠0,a、b、c为常数),则称y为x的二次函数;如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两台智能机器人从同一地点P出发,沿着笔直的路线行走了450cm到点Q.甲比乙先出发,乙出发一段时间后速度提高为原来的2倍.甲匀速走完全程.两机器人行走的路程y(cm)与时间x(s)之间的函数图象如图所示.根据图象所提供的信息解答下列问题:
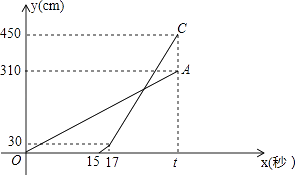
(1)乙比甲晚出发秒,乙提速前的速度是每秒cm,t=;
(2)当x为何值时,乙追上了甲?
(3)若两台机器人到达终点Q后迅速折返,并保持折返前的速度继续匀速行走返回到点P,乙比甲早到多长时间? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,AO⊥BC,DO⊥OE.
(1)不添加其他条件情况下,请尽可能多地写出图中有关角的等量关系(至少3个);
(2)如果∠COE
 350,求∠BOD的度数.
350,求∠BOD的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国曾五次实施药品降价,累计降价的总金额为269亿元,五次药品降价的年份与相应降价金额如下表所示,表中缺失了2003年、2007年相关数据。已知2007年药品降价金额是2003年药品降价金额的6倍,结合表中信息,求2003年和2007年的药品降价金额。
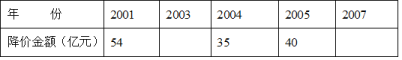
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 ABC中,BO、CO分别平分∠ABC和∠ACB.计算:
ABC中,BO、CO分别平分∠ABC和∠ACB.计算:(1)若∠A
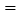 60°,求∠BOC的度数;
60°,求∠BOC的度数;(2)若∠A
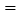 100°, 则∠BOC的度数是多少?
100°, 则∠BOC的度数是多少?(3)若∠A
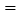 120°, 则∠BOC的度数又是多少?
120°, 则∠BOC的度数又是多少?(4)由(1)、(2)、(3),你发现了什么规律?请用一个等式将这个规律表示出来.
-
科目: 来源: 题型:
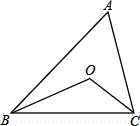
查看答案和解析>>【题目】如图,在已知的ABC中,按以下步骤作图:
①分别以B,C为圆心,以大于 BC的长为半径作弧,两弧相交于两点M,N;
BC的长为半径作弧,两弧相交于两点M,N;
②作直线MN交AB于点D,连接CD.若CD=AC,∠A=50°,则∠ACB的度数为( )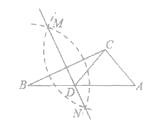
A.90°
B.95°
C.100°
D.105° -
科目: 来源: 题型:
查看答案和解析>>【题目】下面我们做一次折叠活动:
第一步,在一张宽为2的矩形纸片的一端,利用图(1)的方法折出一个正方形,然后把纸片展平,折痕为MC;
第二步,如图(2),把这个正方形折成两个相等的矩形,再把纸片展平,折痕为FA;
第三步,折出内侧矩形FACB的对角线AB,并将AB折到图(3)中所示的AD处,折痕为AQ.
根据以上的操作过程,完成下列问题:
(1)求CD的长.
(2)请判断四边形ABQD的形状,并说明你的理由.
相关试题

