【题目】如图,在已知的ABC中,按以下步骤作图:
①分别以B,C为圆心,以大于 ![]() BC的长为半径作弧,两弧相交于两点M,N;
BC的长为半径作弧,两弧相交于两点M,N;
②作直线MN交AB于点D,连接CD.若CD=AC,∠A=50°,则∠ACB的度数为( )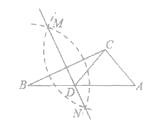
A.90°
B.95°
C.100°
D.105°
参考答案:
【答案】D
【解析】解:∵AC=CD,∠A=50°,
∴∠ADC=∠A=50°,∠ACD=180°-2∠A=80°.
由MN的作法可得MN是BC的垂直平分线,
∴CD=BD,
∴∠BCD= ![]() ∠ADC=25°,
∠ADC=25°,
则∠ACB=∠ACD+∠BCD=80°+25°=10°.
故选:D.
【考点精析】根据题目的已知条件,利用三角形的外角和线段垂直平分线的性质的相关知识可以得到问题的答案,需要掌握三角形一边与另一边的延长线组成的角,叫三角形的外角;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角;垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国曾五次实施药品降价,累计降价的总金额为269亿元,五次药品降价的年份与相应降价金额如下表所示,表中缺失了2003年、2007年相关数据。已知2007年药品降价金额是2003年药品降价金额的6倍,结合表中信息,求2003年和2007年的药品降价金额。
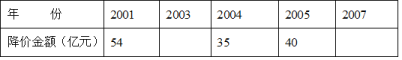
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y1=﹣ax2+2ax﹣a﹣3(a>0)和y2=a(x+1)2﹣1(a>0)的顶点分别为M、N,与y轴分别交于E、F.

(1)①函数y1=﹣ax2+2ax﹣a﹣3(a>0)的最大值是;
②当y1、y2的值都随x的增大而增大时,自变量x的取值范围是;
(2)当EF=MN时,求a值,并判断四边形EMFN是何种特殊的四边形;
(3)若y2=a(x+1)2﹣1(a>0)的图象与x轴的右交点为A(m,0),当△AMN为等腰三角形时,求方程a(x+1)2﹣1=0的解. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 ABC中,BO、CO分别平分∠ABC和∠ACB.计算:
ABC中,BO、CO分别平分∠ABC和∠ACB.计算:(1)若∠A
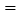 60°,求∠BOC的度数;
60°,求∠BOC的度数;(2)若∠A
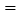 100°, 则∠BOC的度数是多少?
100°, 则∠BOC的度数是多少?(3)若∠A
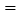 120°, 则∠BOC的度数又是多少?
120°, 则∠BOC的度数又是多少?(4)由(1)、(2)、(3),你发现了什么规律?请用一个等式将这个规律表示出来.
-
科目: 来源: 题型:
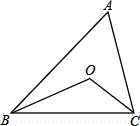
查看答案和解析>>【题目】下面我们做一次折叠活动:
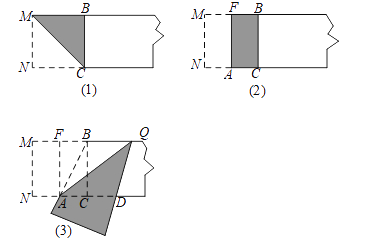
第一步,在一张宽为2的矩形纸片的一端,利用图(1)的方法折出一个正方形,然后把纸片展平,折痕为MC;
第二步,如图(2),把这个正方形折成两个相等的矩形,再把纸片展平,折痕为FA;
第三步,折出内侧矩形FACB的对角线AB,并将AB折到图(3)中所示的AD处,折痕为AQ.
根据以上的操作过程,完成下列问题:
(1)求CD的长.
(2)请判断四边形ABQD的形状,并说明你的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算下列各题
(1)15+(-
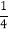 )-15-(-0.25) (2) (-81)÷
)-15-(-0.25) (2) (-81)÷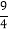 ×
× ÷(-32)
÷(-32)(3)29
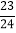 ×(-12) (4)25×
×(-12) (4)25×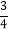 -(-25)×
-(-25)× +25×(-
+25×(-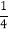 )
)(5)-24-(-4)2 ×(-1)+(-3)3 (6)3.25-[(-
 )-(-
)-(- )+(-
)+(-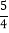 )+
)+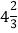 ]
] -
科目: 来源: 题型:
查看答案和解析>>【题目】按要求解答下列各题
(1)已知a、b 互为相反数,c、d 互为倒数,x=(-2)2。
试求x2 -(a + b + c×d) x +(a + b)2015 +(-c×d)2016的值。
(2)已知有理数a、b、c 满足|a-1|+|b-3|+|3c-1|=0,求(a×b×c)178 ÷(a36×b7×c6)的值。
相关试题

