【题目】甲乙两台智能机器人从同一地点P出发,沿着笔直的路线行走了450cm到点Q.甲比乙先出发,乙出发一段时间后速度提高为原来的2倍.甲匀速走完全程.两机器人行走的路程y(cm)与时间x(s)之间的函数图象如图所示.根据图象所提供的信息解答下列问题: 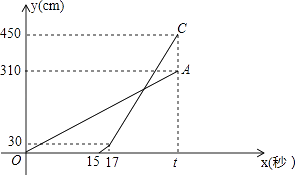
(1)乙比甲晚出发秒,乙提速前的速度是每秒cm,t=;
(2)当x为何值时,乙追上了甲?
(3)若两台机器人到达终点Q后迅速折返,并保持折返前的速度继续匀速行走返回到点P,乙比甲早到多长时间?
参考答案:
【答案】
(1)15;15;31
(2)解:设甲对应的函数解析式为:y=kx,
310=31k,得k=10,
即甲对应的函数解析式为:y=10x,
设乙提速后对应的函数解析式为y=mx+n,
![]() ,得
,得 ![]() ,
,
∴乙提速后对应的函数解析式为y=30x﹣480,
∴ ![]() ,得
,得 ![]() ,
,
即当x为24时,乙追上了甲
(3)解:甲全程用:900÷10=90秒,
乙全程用:31+450÷30=31+15=46秒,
90﹣46=44秒,
即乙比甲早到44秒
【解析】解:(1)由图象可得, 乙比甲晚出发15秒,乙提速前的速度为:30÷(17﹣15)=15cm/s,t=17+(450﹣30)÷(15×2)=31,
所以答案是:15,15,31;
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A=3a2b﹣2ab2+abc,小明同学错将“2A﹣B“看成”2A+B“,算得结果为4a2b﹣3ab2+4abc.
(1)计算B的表达式;
(2)求出2A﹣B的结果;
(3)小强同学说(2)中的结果的大小与c的取值无关,对吗?若a=
 ,b=
,b= ,
,求(2)中式子的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AD=5,AB=8,点E为射线DC上的一个动点,把△ADE沿AE折叠点.D的对应点为D′.
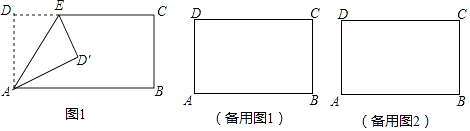
(1)求点D′刚好落在对角线AC上时,D′C的长;
(2)求点D′刚好落在此对称轴上时,线段DE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】小明有5张写着不同的数字的卡片,请你按要求抽出卡片,完成下列各问题:

(1)从中取出2张卡片,使这2张卡片上数字乘积最大,最大值是 ;
(2)从中取出2张卡片,使这2张卡片上数字相除的商最小,最小值是 ;
(3)从中取出4张卡片,用学过的运算方法,使结果为24.写出运算式子:
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,AO⊥BC,DO⊥OE.
(1)不添加其他条件情况下,请尽可能多地写出图中有关角的等量关系(至少3个);
(2)如果∠COE
 350,求∠BOD的度数.
350,求∠BOD的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国曾五次实施药品降价,累计降价的总金额为269亿元,五次药品降价的年份与相应降价金额如下表所示,表中缺失了2003年、2007年相关数据。已知2007年药品降价金额是2003年药品降价金额的6倍,结合表中信息,求2003年和2007年的药品降价金额。
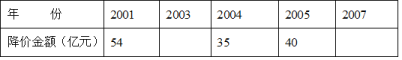
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y1=﹣ax2+2ax﹣a﹣3(a>0)和y2=a(x+1)2﹣1(a>0)的顶点分别为M、N,与y轴分别交于E、F.

(1)①函数y1=﹣ax2+2ax﹣a﹣3(a>0)的最大值是;
②当y1、y2的值都随x的增大而增大时,自变量x的取值范围是;
(2)当EF=MN时,求a值,并判断四边形EMFN是何种特殊的四边形;
(3)若y2=a(x+1)2﹣1(a>0)的图象与x轴的右交点为A(m,0),当△AMN为等腰三角形时,求方程a(x+1)2﹣1=0的解.
相关试题

