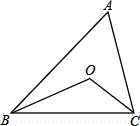
【题目】如图,在![]() ABC中,BO、CO分别平分∠ABC和∠ACB.计算:
ABC中,BO、CO分别平分∠ABC和∠ACB.计算:
(1)若∠A ![]() 60°,求∠BOC的度数;
60°,求∠BOC的度数;
(2)若∠A ![]() 100°, 则∠BOC的度数是多少?
100°, 则∠BOC的度数是多少?
(3)若∠A ![]() 120°, 则∠BOC的度数又是多少?
120°, 则∠BOC的度数又是多少?
(4)由(1)、(2)、(3),你发现了什么规律?请用一个等式将这个规律表示出来.
参考答案:
【答案】(1)∠BOC![]() 120°;(2)∠BOC
120°;(2)∠BOC![]() 140°;(3)∠BOC=150°;(4)∠BOC=90°+
140°;(3)∠BOC=150°;(4)∠BOC=90°+![]() ∠A
∠A
【解析】
(1)根据BO、CO分别平分∠ABC和∠ACB可得: ∠CBO+∠BCO的值,再根据三角形内角和得出∠BOC;
(2)、(3)同理(1)可求得;
(4)根据(1)-(3)规律可得.
(1)∵BO、CO分别平分∠ABC和∠ACB.∠A ![]() 600
600
∴∠CBO+∠BCO![]()
![]() (1800
(1800![]() ∠A)
∠A)![]()
![]() (1800
(1800![]() 600)
600)![]() 600
600
∴∠BOC![]() 1800
1800![]() (∠CBO+∠BCO)
(∠CBO+∠BCO)![]() 1800
1800![]() 600
600![]() 1200
1200
(2)同理,若∠A ![]() 1000, 则∠BOC
1000, 则∠BOC![]() 1800
1800![]()
![]() (1800
(1800![]() ∠A)
∠A)![]() 900+
900+![]() ∠A
∠A![]() 1400
1400
(3)同理,若∠A ![]() 1200, 则∠BOC
1200, 则∠BOC![]() 1800
1800![]()
![]() (1800
(1800![]() ∠A)
∠A)![]() 900+
900+![]() ∠A
∠A![]() 1500
1500
(4)由(1)、(2)、(3),发现:∠BOC![]() 1800
1800![]()
![]() (1800
(1800![]() ∠A)
∠A)![]() 900+
900+![]() ∠A
∠A
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,AO⊥BC,DO⊥OE.
(1)不添加其他条件情况下,请尽可能多地写出图中有关角的等量关系(至少3个);
(2)如果∠COE
 350,求∠BOD的度数.
350,求∠BOD的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国曾五次实施药品降价,累计降价的总金额为269亿元,五次药品降价的年份与相应降价金额如下表所示,表中缺失了2003年、2007年相关数据。已知2007年药品降价金额是2003年药品降价金额的6倍,结合表中信息,求2003年和2007年的药品降价金额。
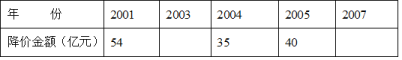
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y1=﹣ax2+2ax﹣a﹣3(a>0)和y2=a(x+1)2﹣1(a>0)的顶点分别为M、N,与y轴分别交于E、F.

(1)①函数y1=﹣ax2+2ax﹣a﹣3(a>0)的最大值是;
②当y1、y2的值都随x的增大而增大时,自变量x的取值范围是;
(2)当EF=MN时,求a值,并判断四边形EMFN是何种特殊的四边形;
(3)若y2=a(x+1)2﹣1(a>0)的图象与x轴的右交点为A(m,0),当△AMN为等腰三角形时,求方程a(x+1)2﹣1=0的解. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在已知的ABC中,按以下步骤作图:
①分别以B,C为圆心,以大于 BC的长为半径作弧,两弧相交于两点M,N;
BC的长为半径作弧,两弧相交于两点M,N;
②作直线MN交AB于点D,连接CD.若CD=AC,∠A=50°,则∠ACB的度数为( )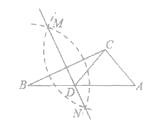
A.90°
B.95°
C.100°
D.105° -
科目: 来源: 题型:
查看答案和解析>>【题目】下面我们做一次折叠活动:
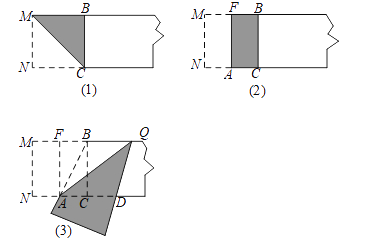
第一步,在一张宽为2的矩形纸片的一端,利用图(1)的方法折出一个正方形,然后把纸片展平,折痕为MC;
第二步,如图(2),把这个正方形折成两个相等的矩形,再把纸片展平,折痕为FA;
第三步,折出内侧矩形FACB的对角线AB,并将AB折到图(3)中所示的AD处,折痕为AQ.
根据以上的操作过程,完成下列问题:
(1)求CD的长.
(2)请判断四边形ABQD的形状,并说明你的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算下列各题
(1)15+(-
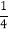 )-15-(-0.25) (2) (-81)÷
)-15-(-0.25) (2) (-81)÷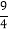 ×
× ÷(-32)
÷(-32)(3)29
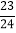 ×(-12) (4)25×
×(-12) (4)25×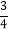 -(-25)×
-(-25)× +25×(-
+25×(-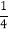 )
)(5)-24-(-4)2 ×(-1)+(-3)3 (6)3.25-[(-
 )-(-
)-(- )+(-
)+(-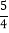 )+
)+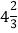 ]
]
相关试题

