搜索
【题目】如图，已知四边形ABCD是正方形，E、F分别是DC和CB的延长线上的点，且DE=BF，连接AE、AF、EF．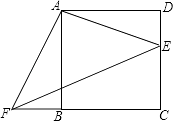 
（1）填空：△ABF可以由△ADE绕旋转中心点 ， 按逆时针方向旋转度得到；
（2）若BC=8，DE=6，求△AEF的面积．
参考答案：
【答案】
（1）A；270
（2）解：∵四边形ABCD是正方形，BC=8，
∴AD=8，
在Rt△ADE中，DE=6，AD=8，
∴AE= 
=10，
∵△ABF可以由△ADE绕旋转中心 A点，按顺时针方向旋转90 度得到，
∴AE=AF，∠EAF=90°，
∴△AEF的面积= 
AE2= ×100=50（平方单位）．
【解析】解：（1）△ABF可以由△ADE绕旋转中心点A，按逆时针方向旋转 270度得到．所以答案是：A，270；
【考点精析】通过灵活运用旋转的性质，掌握①旋转后对应的线段长短不变，旋转角度大小不变；②旋转后对应的点到旋转到旋转中心的距离不变；③旋转后物体或图形不变，只是位置变了即可以解答此题．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图是二次函数y=ax2+bx+c图象的一部分，图象过点A（﹣3，0），对称轴为直线x=﹣1，给出四个结论，其中正确结论是（ ）
A.b2＜4ac
B.2a+b=0
C.a+b+c＞0
D.若点B（
，y1）、C（ 
，y2）为函数图象上的两点，则y1＜y2 -
科目： 来源： 题型：
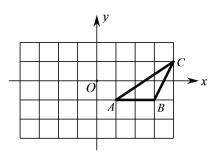
查看答案和解析>>【题目】如图，△ABC 顶点的坐标分别为 A (1，－1)、B（3，－1）、C（4，1）．
⑴将△ABC向上平移1个单位，再向左平移1个单位，请画出平移后得到的△A1B1C1并写出点 A1、B1、C1 的坐标；
⑵若△A1B1C1 与△A1B1D 全等（D 点与 C1 不重合），直接写出点D的坐标．
-
科目： 来源： 题型：
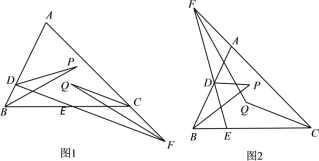
查看答案和解析>>【题目】已知D、E分别为△ABC中AB、BC上的动点，直线DE与直线AC相交于F，∠ADE的平分线与∠B的平分线相交于P，∠ACB的平分线与∠F的平分线相交于Q．
（1）如图1，当F在AC的延长线上时，求∠P与∠Q之间的数量关系；
（2）如图2，当F在AC的反向延长线上时，求∠P与∠Q之间的数量关系（用等式表示）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，A(a,b)，B(c,0)，|a-3|+(2b-c)2+
=0.
(1)求点A，B的坐标；
(2)如图，点C为x轴正半轴上一点，且OC＝OA，点D为OC的中点，连AC，AD，请探索AD＋CD与
AC之间的大小关系，并说明理由；
(3)如图，过点A作AE⊥y轴于E，F为x轴负半轴上一动点（ 不与(－3,0)重合 ），G在EF延长线上，以EG为一边作∠GEN＝45°，过A作AM⊥x轴，交EN于点M，连FM，当点F在x轴负半轴上移动时，式子
的值是否发生变化？若变化，求出变化的范围；若不变化，请求出其值并说明理由.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在水平地面点A处有一网球发射器向空中发射网球，网球飞行路线是一条抛物线，在地面上落点为B．有人在直线AB上点C（靠点B一侧）竖直向上摆放无盖的圆柱形桶，试图让网球落入桶内．已知AB=4米，AC=3米，网球飞行最大高度OM=5米，圆柱形桶的直径CD为0.5米，高为0.3米（网球的体积和圆柱形桶的厚度忽略不计）．
（1）如图，建立直角坐标系，求此抛物线的解析式；
（2）如果竖直摆放7个圆柱形桶时，网球能不能落入桶内？
（3）当竖直摆放圆柱形桶至多多少个时，网球可以落入桶内？ -
科目： 来源： 题型：
查看答案和解析>>【题目】已知，如图，直线l经过A（4，0）和B（0，4）两点，抛物线y=a（x﹣h）2的顶点为P（1，0），直线l与抛物线的交点为M．
（1）求直线l的函数解析式；
（2）若S△AMP=3，求抛物线的解析式．
相关试题
